Matematyka 2 47

346 V. Elementy rachunku pra^ilu/toduhieturua

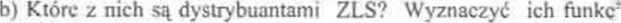
pr-stwa.

c) Klóre z nich są dystrybuantami ZLC? Podać postać GP 13. Dobrać tak stałe a i b. aby funkcje postaci

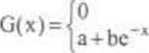
dla x<0 dla x>0

0    dla x<0 F(x)=4ax² dla 0<x£2

1    dla x>2.

były dystrybuantami: a)ZLS. b)ZLC.

14. ZLC X ma rozkład prostokątny skoncentrowany na przedział (0.1). tj rozkład zadany GP postaci:

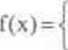
I dla 0<x<l 0 dla x £ 0 v x > I

sprawdzić, że różna od niej ZL Y = 1 - X ma taką samą GP. a więc i taki sam rozkład pr-stwa.

15. Funkcja f_x(x) =

0 dla x < 0 e"^x dla x>0

jest GP ZL X. Wyznaczyć

dystrybuantę i GP ZL Y. jeśli Y= Vx.

Odpowiedzi.

I a)c-0,3, dl p,=0,1, p₂ =0, pj=U,5. p₄ =1, p, = 0.X. p*=0.4. p_T-0.5.

P*=0,6, p, =0,9.

X,	-^1 2	0	4	9	15
p,	1 0.2	0.2	0,3	0.1	0.2

5. I ^9	II	13	15 6.	*< | /J/4 17/3/2		)/I/4
P. I 1/35	12/35	18/35	4/35	p, | 0,3 |	0.6	0.1
7. a) a-l. b) x	II (-*.0>		(0.1 >	(l.2>	(2.x)
F(x)		0		~x^J +2x-1	1

c) p, ^0,5. p, =0.75, Pi -1/8. p₄ = pi

K. b)	x 1 (-‘».0>	(O.R>	(«.»)
	F(x) | U	sin^-x	1

«) p, =1/72 *0.71, pj = 1/2,

9

a) F(x)=

0    dla    x fi—I,

<x^J+l)/v dla -1<xfi2,

1    dla    x>2:

p,=F(l)«2/9. p, = KI)-F(0)=l/9.

b) F(x) =

0    dla x fi 0. I(x-l)³t-l]/2dla0<xfi2,

1    dla x > 2,

p, = l'(0^<X<U)=l/K.

p_, =|-p, =7/8

c) F(x)~

0    dbxfiO, x⁴/l6 dla 0<xfi2,

1    dlax>2;

p, = l-P(0.5<X <1,5^5/16.

p_? = l pi — 11/16.

^d)

dla x<l, dla x>l;

_Pl - F(3)=2/3,

P; =1- F(2) = l/2

c) F(x)

0    dlii \ fi I,

I- l/x² dla x>J;

p,=F(2)-H-2» = V4. p,=P(X<0 v X>41= 1/16.

0 F(x)»

0    dla x<l,

/x -I dla I<xfi4.

1    dla X >4;

Pi «F(4) — F(2)—2— /T »0,59. p_: = F<-2)*F(2)-F<0)=/2-l*0.49.

g)F(x)

0    dU xfi0,

l-e ^ł* dla x>0;

p, -!*OC>l)«c“² *0,135,

p» - P(0<X<l| + P(X>2)=l-e*‘ +■ c ⁴ *0.883

1

   a> p, = I-F(b). p_: = F(b*), p,=.F(b*)-F(a*),    — F(b*)-F(a).

Pj = F(b)-F(a').

b)    p, = l-F(b). Pj = F(b), pi = p₄ -Pj- F(b)-F(a)

c)    p, =0.8. p_:=0.6. p, = 0.1

2

   y, | Q |    2    3 X, Y są różnymi ZL. bo np X(w,) = 0*

Pj I 1/8    3/8    3/8    1/8    *Y«a,) = 3;

jednakowe funkcje pr-stwa (a więc jednakowe rozkłady pr-siwa|.