Matematyka 2 65

364 V Elementy rachunku pruwdnpodohiethlwu

ZL o rozkładzie jednopunktowym jest modelem dla wielkości, które po bliższej analizie okazują się wielkościami zdeterminowanymi; umożliwia traktowanie wielkości zdeterminowanych jako wielkości losowych.

Zmienna o rozkładzie zero-jedynkowym.

Mówimy, że ZLS X ma rozkład zero-jedynkowy z parametrem p,

0<p<l, co zapisujemy X~(0-l)_p, jeśli ma tylko dwa punkty skokowe

x, = lix₃=0 i skoki odpowiednio p oraz q = I - p. Zatem jej funkcja pr-stwa p( ) i dystrybuanta F są postaci:

X,	o	i . *	(-ac.0>	(0.l>	(i.»)
p(*.)	q	P F(x)	0	q	i

Wartość oczekiwana i wariancja ZL X o rozkładzie (0-1 )_p wyrażają się wzorami:

(5.1)    EX = p, VarX=pq.

Równości te otrzymujemy na podstawie definicji:

EX=0*q+lp»p,

VarX=*(0-p)^J q+(l-p)²-p=p^Jq+q²p = pq(p+q)*pq.

ZL o rozkładzie (0- l)_p jest modelem dla doświadczenia losowego. w którym wyniki klasyfikujemy jako "mające daną cechą W" z pr-stwem p i "nie mające tej cechy" z pr-stwem q. W szczególności jest użyteczna przy sprowadzaniu cech jakościowych do cech ilościowych.

PRZYKŁAD 5.1. Partia towaru składa się zc sztuk zgodnych z normą i pozostałych (wymagania mogą dotyczyć również cech jakościowych. np. koloni). Niech ZL X przyjmuje z pr-stwem p wartość I. gdy sztuka towaru jest zgodna z normą, oraz z pr-stwem q wartość 0. gdy nic jest z mą w^r zgodzie. Tak określona ZL ma rozważany tu zerojedynkowy rozkład pr-stwa z nieznanym parametrem p.    ■

ZMIENNA O ROZKŁADZIE DWUMIANOWYM. Niech p oznacza daną liczbę z przedziału (0,1), n - daną liczbą naturalną, n e N. Mówimy, że ZI,S S„ ma rozkład dwumianowy (binomialny, Bernoul-Iłego) 7. ,..'^rametrami (n.p), co zapisujemy S„ -b(n.p), gdy jej punkty skokowe x_ksk tworzy zbiór W= {0,1,2,....nj a skoki p_kł czyli pr-stwu P(S_n = k), wyrażają się wzorem:

(5.2) p_k*P(S„ = k)=(£)py-^k. k = 0.l.....n; 0<p<l, q = I-p

Pr-stwa (5.2)są kolejnymi wyrazami rozwinięcia n-lcj potęgi dwumianu (q+p)ⁿ:

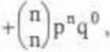
k„ ił-k

(q+p)" =(o)^p°^{qn +}(")^p'^{qn, + +}(k]i^,Łq

stad nazwa - rozkład dwumianowy. Ponadto z ostatniej równości, wobec (q + p)“ * I" = 1, widać, żc pr-stwa p_k spełniają warunek unormowania:

Po+P.⁺ "⁺P, ^{= I}

Rozważana tu ZL S„ wiąże się ze znanym ze szkoły schematem Bemoulliego. Przypomnijmy; ciąg doświadczeń Dj.Dj.—.D,, nazywamy schematem Bernoulliego (schematem n prób Bernoulliego). jeśli: 1) w każdym z tych doświadczeń może zajść zdarzenie A (zajście zdarzenia A nazywa się sukcesem, niczajście - porażką). 2) pr-stwo zajścia zdarzenia A (czyli pr-stwo sukcesu) w każdym pojedynczym doświadczeniu D, jest jednakowe (powiedzmy p),    3) doświadczenia

D„D_:y.D_n są niezależne (w tym sensie, że wynik każdego doświadczenia D, jest niezależny od wyników pozostałych doświadczeń).

A oto zapowiedziany związek: ZL S_n o rozkładzie dwumianowym b(n.p) można interpretować jako możliwą liczbę sukcesów w schemacie n doświadczeń Bernoulliego z pr-stwem p sukcesu w pojedynczymi doświadczeniu D_{. Tym samym pr-stwa p_Ł dane wzorem (5.2) można interpretować jako pr-stwa uzyskania k sukcesów w dowolnej kolejności u n takich doświadczeniach.

Prawdziwa jest jeszcze jedna zależność. ZL S_n o rozkładzie dwumianowym b(n.p) jest sumą n niezależnych ZL X_l,X_:.--,X_n o tymi samym rozkładzie (0-l)_p:

(5.3)    S_lł*X, + X₂+ *** +X„.    X,~(0-l)_p

Istotnie. Niech bowiem dla i=1,2.....n, X, oznacza ZL przyj

mującą wartość I albo 0 stosownie do tego, czy w doświadczeniu D, zrealizowało się zdarzenie A (sukces), czy też zdarzenie przeciwne A'