skanuj0065 (Kopiowanie)

gicznych okresach półtrwania podawanego leku) i wyrażenie e~’^,KT staje się praktycznie równe zero. W tych warunkach wyrażenia 8.43-8.44a uproszczają się i przyjmują postać, jak niżej:

^} 1—e^-KT	(8.45)
1 » i_e-KT	(8.45a)
I—e^-KT	(8.46)
’ 1 —e~^KT	(8.46a)

Korzystając z nich można obliczyć ekstremalne (maksymalne i minimalne) stężenie substancji leczniczej w osoczu po w-tej dawce lub to samo stężenie w osiągniętym stanie stacjonarnym. Wykonanie takich obliczeń ułatwia znakomicie użycie kalkulatorów elektronicznych pozwalających na szybkie określenie wartości wyrażenia e~\

Duże znaczenie w rozważaniach ilościowych nad procesem kumulacji leku ma tzw. średnie stężenie substancji leczniczej w stanie stacjonarnym (C), określane przez Wagnera następującym równaniem:

w którym:

J Cdr — pole pod krzywą stężenie—czas, mierzone w czasie równym przedziałowi dawkowania t po osiągnięciu stanu stacjonarnego.

Iloczyn tak określonego stężenia C przez objętość dystrybucji daje średnią ilość substancji leczniczej w stanie stacjonarnym A. Dla obliczenia tej ilości oraz stężenia C wystarczy nawiązać do omawianego na str. 122 stanu stacjonarnego osiąganego w czasie wlewu dożylnego prowadzonego z szybkością k„. Traktując dożylne podawanie dawki D w przedziałach czasu t (jako podawanie ze średnią szybkością k₀ = Z)/t) można przyjąć, że w wyniku tego podawania ustali się w osoczu jakieś średnie stężenie stacjonarne C. Podstawiając w równaniu 8.38: Cl, = K • Va i k„ = Z)/t otrzymuje się po prostych przekształceniach:

*- Ł    <⁸-⁴⁸⁾

128 Zarys biofarnuuji

Za pomocą tej wielkości Wagner określił tzw. współczynnik kumulacji R zdefiniowany równaniem:

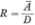
u więc stosunkiem średniej ilości substancji leczniczej w stanie stacjonarnym do podanej dawki £>. Wprowadzając do tego równania wartość A, określoną równaniem 8.48 i wyrażając stalą szybkości eliminacji przez odpowiadający jej okres półtrwania, otrzymuje się po prostych przekształceńiach następujące wyrażenie, pozwalające ocenić ilościowo proces kumulacji:

lub

(8.49)

w którym:

c ■» t/10,5 — tzw. względny przedział dawkowania.

Jak łatwo zauważyć z tego wyrażenia współczynnik kumulacji R zwiększa się wraz ze zmniejszeniem się wartości e, albo rozumując inaczej im mniejsze jest e, tym silniej zaznacza się kumulacja leku.

2

C [mg/1]

vNKN!

,Z-2h

Z=6h

0

16 2i 32 J Chi

Ryc. 8.13. Przebieg zmian stężenia hipotetyczne) substancji leczniczej w osoczu po wielokrotnym podaniu dawki D w przedziałach czasu t, = 8 h i x, «= 2 h. Zmiana przedziału czasu powoduje zmianę wartości z i tym samym zmianę współczynnika kumulacji

Na rycinie 8.13 przedstawiono przebieg kumulacji hipotetycznej substancji leczniczej o okresie półtrwania r_os = 5 n podawanej w 2 różnych przedziałach czasu t. W przypadku, gdy r = 8 h (e = 1,06) kumulacja jest znikomo mała. W przypadku t - 2 h (e = 0,4) kumulacja tej substancji leczniczej jest wyraźna. Jak z tego wynika, stopień kumulacji nie jest jakąś właściwością substancji leczniczej (podział leków na kumulujące się i nie kumulujące się jest błędny), ale zależy tylko i wyłącznie od stosunku przedziału czasu między podaniem kolejnych dawek do biologicznego okresu półtrwania podawanej substancji leczniczej.

Dożylne podawanie substancji leczniczych 129

• - Zarys biofarmacji