SWScan00070

126 Kontrakty tejmmowb i opcje

4 -

*    Ornlt m¹(v

t« trticty

-1-:-1-‘-►

12    3    4$

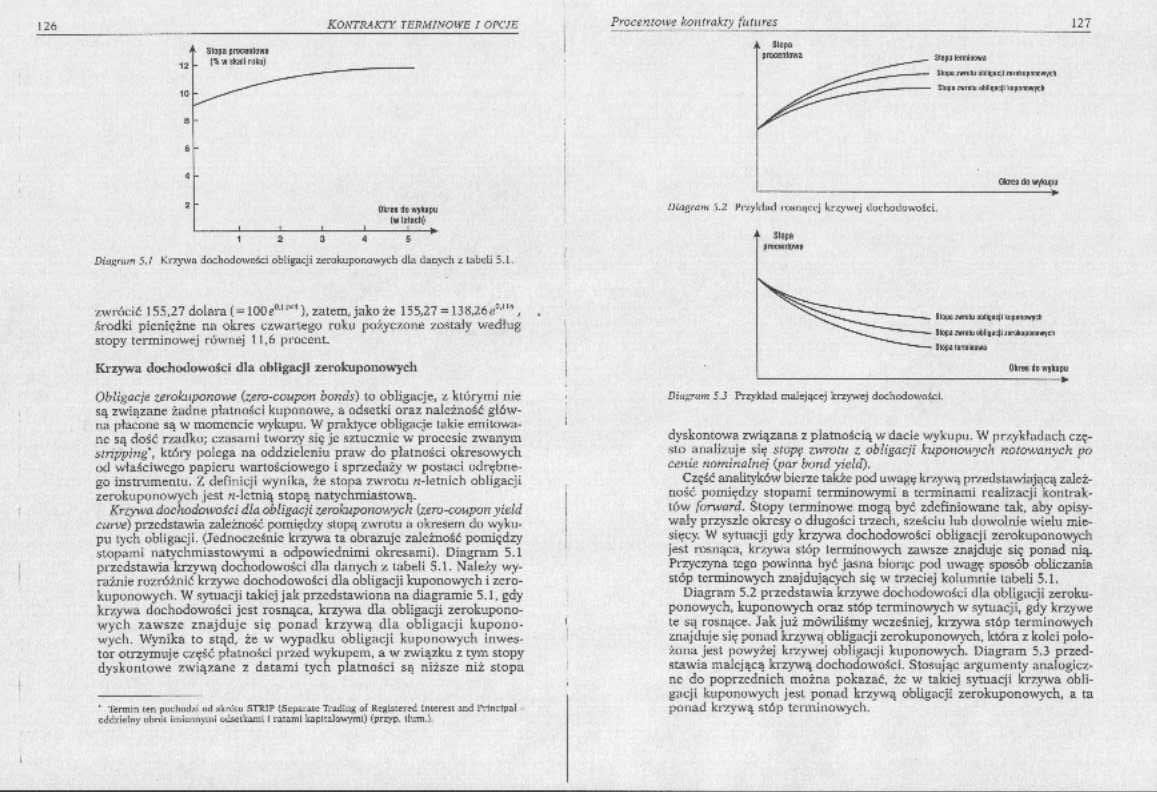
JMtutmm 5Krzywa ir»;hod<nvc£a obligacji znrakupor^i^ycb dla Uacycii z Litidj 3.1 /.wrócić 155,27 dolara ( = 100r^Wpr1). zatem, jako że 155,27 = 13820 środki pieniężne rut okres czwartego roku pożyczone zostały według stopy terminowej równej 11.6 procent.

Krzywa dochodowości dla obligacji zernkuponowych

Obligacja z²rohipor>o>vt faro-coupon bonds) to obligucje, z którymi nie są związane żadne płatności kuponowe, a odsetki oraz należność główna płacone są w momencie wykupu. W praktyce obligacje lukie emitowane są dość rzadko; czasami tworzy się je sztucznie w procesie zwanym *trtyp\n%, który polega na oddzieleniu praw do płatności okresowych od właściwego papieru wartościowego i sprzedaży w postaci odrębnego instrumentu. /. definicji wynika, >.e stopa zwrotu «-letnich obligacji zeroku po nowych jest «²lcmią stopą natychmiastową.

Krtywo. dochodowości dla obligacji yerokuponawyck iztro-coupon yitid curve) przedstawia zależność pomiędzy stupą zwrotu it okresem do wykupu tych obligacji. (Jednocześnie krzywa ta obrazuje zależność pomiędzy stopami natychmiastowymi a odpowiednimi okresami). Diagram 5.1 przedstawia krzywą dochodowości db danych /. tabeli S.l. Mależ.y wyraźnie rozróżnić krzywo dochodowości dla obligacji kuponowych i zero-kuponowych. W sytuacji takiej jak przedstawiona na diagramie 5.1. gdy kr/.ywa dochodowości jest rosnąca, krzywa dla obligacji zerokuponowych zawsze znajduje się ponad krzywą dla obligacji kuponowych. Wynika to stąd. że w wypadku obligacji kuponowych inwestor otrzymuje część płatności przed wykupem, a w związku z tym stopy dyskontowe związane z datami tych płatności są niższe niż stopa

Gtoci OJ WĄX|I1

HuIgc-Oh \.2 Hr/ykliuł taMM|ci-j kr*ywcj OwboCJMOicL ¹ JMf*

inantMI

i ,    «*i*

Slfl MrtrM

Uu rmli nuci m ni >    |

nuniiiJlui uprali

ll Juk Mtti U|I«I Uinnri H|«lwHiO|ijurA*wnu lK«J

Okna li miii [u

---►

DżuzrwK SJ Przykład cuiisjącei icntywej dochodowatcl.

dyskontowa związana z płatnością w dacie wykupu. W przykładach często armllzuje się Stopę zwrotu z obligacji kuponowych notowanych po Cifnu; nominalnej (par front/ yicltl),

Część analityków bierze także pod uwagę krzywą przedstawiającą zależność pomiędzy stopami terminowymi a terminami realizacji kontraktów ftrrward. Stopy terminowe mogą być zdefiniowane tak. aby opisywały przyszłe okresy o długości trzech, sześciu lub dowolnie wielu miesięcy W sytuacji gdy krzywa dochodowości obligacji zcrokuponowych jest rosnąca, krzywy stóp terminowych zawsze znajduje się ponad nią. Przyczyna tego powinna być jasna biorąc pod uwagę sposób obliczania stóp terminowych znajdujących się w trzeciej kolumnie tabeli 5.1.

Diagram 5.2 przedstawia krzywe dochodowości dla obligacji zcrokuponowych. kuponowych oraz stóp terminowych w sytuacji, gdy krzywe te są rosnące. Jak już mówiliśmy wcześniej, krzywa stóp terminowych znajduje się ponad krzywą obligacji zcrokuponowych. która z kolei polo-żłina jest powyżej krzywej obligacji kuponowych. Diagram 5.3 przedstawia msiejącą krzywą dochodowości. Stosując argumenty analogiczne do poprzednich można pokazać, że w takiej sytuacji krnnea obligacji kuponowych jest ponad krzywą obligacji zerokuponowych. a ta ponad krzywą stóp terminowych.

1

cdfTwlny nhnu bwinwqM>l wo<u^r_. l raaunl ^apciia-wymii iprryp. ihan.1-

2

lermn t²r\ pm hmO- ml ²lV<u STU? tSep^-ac n-JuS-g ai RfjiL&UTjć tiueren «d ftlnctpal