SWScan00074

134

KONTRAKTY TLRA*/.VOW£ / OPCJE

-A^sUsp.it n& końcu kolejnych olutión półrocznych ai do koóca dwudziestego roku, kiedy uj zostanie wypłacony nominał obligacji. Wtpółrryrmik kor.wemji nhliczymy dla 100 dotnrów wartości nominalnej ubtieacji. Biorąc pod uwagę. be Stopo dyskontowa jest równa 8 procent w tkali roku przy kapitalizacji półrocznej (lub 1 procent w shr.U póh ocznej). wartom obligacji wyniesie;

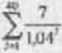
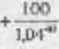
*159.311

l*o podzieleniu |>rw*7 wartość nominalną obligacji otrzymamy współczynnik koUWCTSji równy 1.5938.

2. Rn/ważmy obUg&c.ę kuponową O oprocentowaniu 14 procent, n okresie do wykupu jó Witym I^ Int i cztery miesiące. W celu obliczenia wspułczy nuik* konwersji zakładamy, re okres do wykupu tej obligacji Jest rów^iy dokładnie 18 iat i trzy miesiące. Po zdyskontowaniu wszystkich przyszłych płatności wynikających z obligacji na d»eń przypadający za uijr miesiące od dzisiaj otrzymamy wartość:

* J°<L

1.04-    1.04“

ll _n

Y

u i ni-

163.73

W rozważanym przykładzie stopa procentowa dla okicsu ttzymicslęczncflo wynosi 1.9804 procent (= Jw -1 ). W ten sposób. dyskontu jąc wartość ohUgncgi do dnia dzisiejszego, otrzymamy wielkość 160.55 (= 163.73/1,019 K04). Po od jęciu narosłych odretrk u- wysokości 3.5 wartość la wyniesie 1S7.05, a wJęc współczynnik konwersji jcsl równy 1.5705.

Rozliczenie kontraktu futurę*

przy pomocy najtaAttycb z dostępnych obligacji

W każdym momencie istnieje około trzydziestu różnych obligacji, które mogą być dostarczona na warunkach kontraktu futuns notowanego na CBOT Różnią się one zarówno pi>d względem płatności kuponowych, jak 1 okresu do wyicupu. e niekiedy różnice te «ą bardzo znacz;(ca. Si runa zajmująca pozycję krótką rnoża w celu rozliczenia kontraktu dostarczyć nnjwńNze z dostępnych obligacji spełniające jego warunki. Ponieważ strona ta w wyniku wykonania kontraktu otrzymuje:

/Aktualny kurs \ terminowy

■t- Narosłe odsetki

Współczynnik | konwersji J

a cena nabycia obligacji jest równa;

Kurs obligacji + Narosłe odsetki ruijtaószą w dostawie jest obligacja, dla której:

Kurs obligacji -    ^ x ^W?f"'^{A v}>'^nmk]

^{K J} { terminowy    konwersji )

osiąga wartość najniższą. Obliczenia takie należy przeprowadzić dla wszystkich obligacji po kolei.

Pmccniowt koitirakiy futurss		135
lóbtła 5A I3till23ic> tm^ąoc l«W prvr<Wvfrtii .lix.ir.uy		w przedstawionym prjyklaćr<.
Obligacja	Kur * obligacji	Współczynnik konwensji
1	99.SU	1.0382
2	1*13,50	1.5188
.3	119.75	1.2615

Przykład

Tnwetuir ujmujący pozycję kniua zdecydował >ię ua dostawy l próbuje *yb-rać pomiędzy trz^uiadostępnymi obligacjami opisanymi w tabeli 5.4. Zjiłńżmy, że aktualny kun lenuJnowy ic*t równy 93-03, czyli 93,25. Koszty dostawy puizeucgóljiych Obligacji wynoszą:

< )bl igucja 1:    99.5 - (93.25 X 1.03 82) - 2.69

Obligacja*    1435- (93.2.5 x!,5l 88) = 1*7

UbUgocw 3:    119,75 - (93,25x '2615) = 2.12

Wynik* z tego. żę najtańszy do dostarczenia jest obligacja 2.

O tym. którą obligacja jest tańsza do dostarczenia, decyduje kilka czynników. Jeś',j rentowność obligacji prze wy ż*** 8 procent, system obliczania współczynnik* konwersji powoduje, że faworyzowane są długoterminowe obligacje o niskim nprooentowatilu. Gdy natomiast rentowność jest niższa niż B procent, inwestorzy preferują obligacje o krótkim okresie do wykupu, ale u wyższym oprocentowaniu. Jeśli krzywa dochodowości jest rosnąca, preferowane są obligacje o dłuższym ukre-sie do wykupu, jeśli natomiast krzywa opada, pojawia się tendencja do dostarczaniu «>bligtKj: o krótszym okresie d<i wykupu Wreszcie, niektóre obligacje są często sprzedawane powyżej swojej wnrtości teoretycznej. Przykładami taktclt walorów są obligacje o niskim oprocentowaniu oraz obligacje, które przeszły operację .rin/min^u. czyli oddzielenia notowań nominału i płatności’ kuponowych. Jest mało prawdopodobne, by w jakichkolwiek okolicznościiic.lt obligacje tego rodzaju okazały się najtańsze do dostarczenia.

Opcja wUd catj play

Notowania kontraktów futur*% na długoterminowe obligacje skarbowe nu CBOT kończą się o godzinie 14.00 {czasu Chicago). Tymczasem sesja dla obligacji skarbowych na rytiku gotówkowym trwa do 16.00. Co więcej, strona zajmująco pozycję krótką może zawiadomić izbę rozrachunkową giełdy o zamiarze dostawy do godziny 20.00. Jeśli zawiadomienie takie zostanie wystosowane, cena faklnrowu obliczana jest na podstawie ceny naliczenia / danego dnia. a więc ceny zawarcia transakcji tuż przed dzwonkiem kończącym sesję o godzinie 14.00.