Xerox Phaser200MFP 081126113937

116 Janusz Buga, Helena Kassyk-Rokicka

bowym wyrazem może być wariancja i odchylenie standardowe składnika resztowego. Mierniki te obliczmy posługując się następującymi wzorami;

i=i

(4.26)

(4.27)

wariancja S² (z) =

n - 2

odchylenie standardowe S(z) = i/s² (z)

Tabl. 19

yt	yt	yi-yi=Zj	A
19,0	17,83	1,17	1,3689
16,8	17,98	-1,18	1,3924
17,4	18,13	-0,73	0,5329
18,3	18,13	0,17	0,0289
17,4	18,89	-1,49	2,2201
21,0	19,64	1,36	1,8496
20,0	19,94	0,06	0,0036
20,8	20,10	0,70	0,4900
22,1	20,25	1,85	3,4225
21,6	21,00	0,60	0,3600
20,4	21,45	- 1,05	1,1025
19,7	21,60	- 1,90	3,6100
20,1	21,91	-1,81	3,3761
26,0	22,51	3,49	12,1801
22,9	23,12	-0,22	0,0484
22,1	23,12	-1,02	1,0404
325,6	325,60	0,00	33,0264

Dokonując odpowiednich obliczeń dla prezentowanego przykładu (tabl. 19) oraz podstawiając odpowiednie liczby do wzorów (4.26) i (4.27) otrzymujemy:

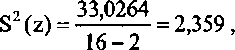
S(z) = V2,359 £1,54,

co oznacza, że średnia zmienność odsetka mieszkańców posiadających samochody, w badanych szestnastu województwach, z tytułu działania innych czynników, poza wysokością produktu krajowego brutto, wynosi 1,54%.

Opisową miarą dopasowania prostej do danych empirycznych jest również współczynnik determinacji liniowej r². W tym przypadku za punkt wyjścia przyjmujemy podział całkowitej zmienności (odchylenia) empirycznej wartości yj względem y na dwa składniki:

y, - y = (9i - y) + (yj - 9 i) dla każdego i = 1,2,n.

Zapisaną równość odczytujemy w następujący sposób: całkowita zmienność (łączne odchylenie) wartości cechy Y względem y równa

się sumie zmienności cechy Y wyjaśnionej regresją (tu liniową) względem cechy X (f(xi)) oraz zmienności Y, która nie została wyjaśniona regresją Y względem cechy X (są to wartości składnika resztowego Zj).

Podnosząc do kwadratu wyrażenia obu stron równości i sumując je dla wszystkich badanych jednostek (i = 1, 2,n), otrzymujemy:

ŻCy* “ y)² = Z(?i - y)² + Ż(ys - h)² >

i=l

(4.28)

co odczytujemy: na całkowitą sumę kwadratów odchyleń wartości cechy Y od ich średniej (y) składa się suma kwadratów odchyleń wartości cechy Y wyjaśnionych regresją Y względem X (pierwszy składnik po prawej stronie równości) i suma kwadratów odchyleń wartości cechy Y nie wyjaśnionych regresją względem cechy X (drugi składnik).

Porównując sumę kwadratów odchyleń wyjaśnioną regresją do całkowitej sumy kwadratów odchyleń, otrzymujemy współczynnik determinacji liniowej r²: