0501

503
§2. Całki niewłaściwe z funkcji nieograniczonych
i istnienie odki niewłaściwej (l)jest równoważne z istnieniem skończonej granicy lim F(b—rj).
1,-0
Jeżeli ta ostatnia istnieje, to naturalne jest przyjęcie jej jako wartości F(b) funkcji pierwotnej dla x = b, uzyskując w ten sposób ciągłość funkcji F(x) w całym przedziale <tz, by. Mamy więc wzór na odkę (1) w jego zwykłej postaci
(5) j f{x) dx = F(b)—F(a) - F(x)\btt.
a
Ten sam wzór jest słuszny także wtedy, gdy punkt osobliwy leży wewnątrz przedziału lub gdy istnieje kilka punktów osobliwych, ale (należy o tym dobrze pamiętać) tylko wtedy, gdy funkcja pierwotna F(x), której pochodną jest wszędzie z wyjątkiem punktów osobliwych funkcja f(x), jest ciągła także w tych punktach osobliwych. Istnienie takiej funkcji pierwotnej jest warunkiem koniecznym istnienia całki niewłaściwej.
Uwaga. „Funkcję pierwotną” F(x) można by rozumieć w nieco ogólniejszym sensie: f(x) musi być pochodną F(x) wszędzie poza punktami osobliwymi i być może jeszcze pewną skończoną liczbą punktów, byleby w tych punktach była zachowana ciągłość funkcji F(x) [porównaj 310].
Zastępując w podstawowym wzorze (5) b przez x, a/(x) przez F'(x) możemy go napisać, tak samo jak w 310, w postaci
X
F(x) =,F(a)+ J F'(x) dx .
a
A więc korzystając z danej pochodnej F'(x) odtwarzamy funkcję pierwotną F(x), jeżeli tylko pochodna ta jest całkowalna, chociażby nawet w sensie niewłaściwym.
Przykłady
8
1) f —. Punkt osobliwy x — 0. Ponieważ funkcja pierwotna y x213 jest ciągła w tym pun--i Y*
kcie, całka istnieje:
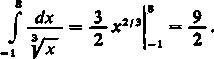
Wyszukiwarka
Podobne podstrony:
499 § 2. Całki niewłaściwe z funkcji nieograniczonych§ 2. Całki niewłaściwe z funkcji
§ 2. Całki niewłaściwe z funkcji nieograniczonych 501 Gdy fal, całka / dx !(*—ff1-*] ma dla ij
505 § 2. Całki niewłaściwe z funkcji nieograniczonych A więc całka jest zbieżna. i 2)
507 § 2. Całki niewłaściwe z funkcji nieograniczonych 483. Przykłady. Zbadać zbieżność całek: * 11)
509 § 2. Całki niewłaściwe z funkcji nieograniczonych Rozwiązanie, (a) Punkty osobliwe: oo i (dla a&
511 § 2. Całki niewłaściwe z funkcji nieograniczonych rt/2 3) Rozpatrzmy następnie całkę rozbieżną
513 § 2. Całki niewłaściwe z funkcji nieograniczonych Jeżeli funkcja f(x) jest parzysta, to / /(jt)
Treść wykładu: Całki niewłaściwe. Szeregi liczbowe. Szeregi potęgowe. Granica i ciągłość funkcji
81 § 1. Definicja i warunki istnienia całki oznaczonej Przy nieograniczonym zmniejszania się wszystk
493 S 1. Całki niewłaściwe o granicach nieskończonych (c) Gdy1-1 1, funkcja podcałkowa ma granicę 0.
506 XIII. Całki niewłaściweJeżeli funkcja f(x) jest bezwzględnie całkowalna w przedziale (a, by, a f
518 XIII. Całki niewłaściwe A Funkcja Jg (x) dx zmiennej A, ciągła w przedziale (a, +oo> ma grani
532 XIII. Całki niewłaściwe 3) Dana jest funkcja f(x) = xe~*. Jest to funkcja monotonicznie malejąca
534 XIII. Całki niewłaściwe 495. Całki Froullaniego. Rozpatrzmy zagadnienie istnienia i obliczenia
542 XIII. Całki niewłaściwe 4) Uogólnić twierdzenie udowodnione w 478, 6) na przypadek, gdy funkcja
556 XIII. Całki niewłaściwe Łatwo można zauważyć, że gdy x -► 0, funkcja podcałkowa dąży do 0, a
420 XXI. Całki niewłaściwe Zadanie 21.3. Obliczyć całkę dx xjx Rozwiązanie. Funkcja podcałkowa
Image279 Ponieważ, tak jak poprzednio, istnieje wiele innych równoważnych postaci tych funkcji, zate
więcej podobnych podstron