0509

511

§ 2. Całki niewłaściwe z funkcji nieograniczonych

rt/2

3) Rozpatrzmy następnie całkę rozbieżną /    (0<k<l). Punktem osobliwym jest a

arc sin k i gdy 0 -*■«, funkcja podcałkowa jest nieskończonością rzędu 1. Mamy

1- In	k—sin 0	= 1 In	sin a—sin 0
j/1 -k^2	1 — k sin 6— }/i—k^2 cos 0	y/l -k^2	1—cos (a—6)

r de

J k—sin 6

Dlatego

“f" + Y i fin sin tx—sin («—ą) , _|n 1-cosw \ o    ^\-k² l    sin(a+ł?)—sin a    sina /'

Gdy ij -*■ 0 wyrażenie pod znakiem logarytmu w pierwszym składniku dąży do 1 (łatwo się można o tym przekonać obliczając nieoznaczoność według reguły de L’Hospitala). Mamy ostatecznie

P. / ■ ~ = -p== in -¹- -    ■ — (0 < * < 1).

J k—sm 0 yl—k²    *

W pewnych przypadkach możemy z góry ustalić istnienie wartości głównej całki. Rozpatrzmy jeden z takich przypadków. Niech będzie dana całka

b

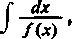
gdzie f(x) jest ciągła w przedziale <a, 6> i przyjmuje wartość zero w jednym tylko punkcie c wewnątrz przedziału. Załóżmy, że w otoczeniu punktu c istnieje pierwsza pochodna f'(x) różna od zera dla x — c, a w samym tym punkcie istnieje także druga pochodna /"(c).

Ponieważ l//(x) jest dla x -*■ c nieskończenie dużą rzędu pierwszego i zmienia przy tym znak przy przejściu x przez c, więc całka niewłaściwa nie istnieje. Wykażemy, że całka ta istnieje w sensie wartości głównej.

Przyjmijmy

1

/(*)

1

f\ć){x-c)

+?>(*)•

Funkcja ta jest ciągła dla x^c. W otoczeniu x — c mamy według wzoru Taylora z resztą w postaci Peano [124]:

/(*) =/'(c) (*—c)+[T(c)+« (x)]- &_^c)* , gdzie a(x) -*• 0, gdy x -+■ c. Wtedy oczywiście

jl/"(c)+<x(x)l

/'(C) |/'(c)+ f%^c>±*S£> (x—c)j

/'(c)(x-c)

a więc <p (x) jest w pobliżu x = c ograniczona, skąd wynika, że jest ona całkowalna nawet w sensie właściwym. Ponieważ istnieje odka w sensie wartości głównej z funkcji _e,_t_^ j____% [patrz 1)], więc to samo

można powiedzieć o naszej całce.