23 (648)

64 II. Parametryczne testy istotności

• 2.19. Dokonano za pomocą sklerometru 42 niezależnych pomialM wytrzymałości gotowych elementów konstrukcji żelbetowych i otrzymaj następujące wyniki (w kG/cm²): 413, ,551, 342, 123, 370, 250, 508, 43|i _:203, 505, 372, 249, 285, 339, 439, 154, 262, 372, 149, 275, 299, 305, IM 320, 460, 392, 436, 272, 263, 379, 309, 432, 358, 453, 416, 454, 374, H 400, 466, 315, 373. Zweryfikować na poziomie istotności a >=.0,001 hipJ tezę, że średnia wytrzymałość gotowych elementów konstrukcji żelbet! wygliwynosi 300 kG/cm². Czy uzyskany wynik jest korzystny dla praktyki K2-20). Dokonano 22 niezależnych pomiarów strat z osypania się ziarr żyta w wylosowanych gospodarstwach rolnych w 1966 r. i otrzymdnólnl stępujące straty (w procentach^: -6;0jj    ^26, 4#1, 6M

5?9£ kń, 6;03,    '5,U, 6/6, 5#1,    ^8V>,49,    83, £1

■&$!, 5,79. Przyjmując poziom istotności a=0,01 zweryfikować hipota że średni procent strat z osypania się ziarna żyta wynosi 5,5. Czy wyjnj testowania jest korzystny dla rolnictwa?

§ 2.2. TEST DLA DWÓCH ŚREDNICH Podstawowe wyjaśnienia

W praktycznych zastosowaniach statystyki zachodzi bardzo często p( trzeba sprawdzenia hipotez dotyczących równości wartości średia w dwóch populacjach normalnych. Typowymi sytuacjami jest tu wspdfl niane już w § 2.1 porównanie proponowanej metody nowej ze starą, p] pulacji zdrowych z populacją chorych itd. Wprawdzie można porównywl też całe rozkłady badanych dwu populacji, ale ze względu na zalety pd stawowego parametru, jakim jest wartość średnia populacji, często ogn niczyć się można do porównania właśnie średnich w dwu populacja W zależności od ilości posiadanych o porównywanych populacja* informacji wyróżnimy trzy modele. W każdym z nich weryfikować moą hipotezę H₀: m_x=m₂, czyli m₁—m₂ =0, gdzie m_t i m₂ oznaczają wartdfl średnie odpowiednio pierwszej i drugiej populacji generalnej. Postać hipl tezy alternatywnej H_x decyduje o rodzaju wybieranego w stosowanya dla hipotezy H₀ teście istotności, jednostronnego lub dwustronnego })| szaru krytycznego.

Model I. Badamy dwie populacje generalne mające rozkłady normalne N(m_x> a^ i N(m₂, <r₂). Odchylenia standardowe <7_X i cr₂ tych populacji si) znane. W oparciu o wyniki dwu niezależnych prób, odpowiednio o li-i/cbnościach i w₂, wylosowanych z tych populacji należy sprawdzić 111 potezę H₀ : m_x=m₂, wobec hipotezy alternatywnej H_x:

Test istotności dla tej hipotezy budujemy następujący sposób. Z wyników prób wylosowanych z tych populacji obliczamy wartości średnich v, i x₂, a następnie wartość statystyki U według wzoru

x_x —x₂

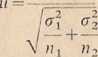
(2.4)

Statystyka ta przy założeniu prawdziwości hipotezy H₀ ma rozkład N(0,\). /. tablicy rozkładu normalnego Ń(0, 1) należy dla przyjętego z góry poziomu istotności a wyznaczyć taką wartość krytyczną u_a, by spełniona była równość P{|t/|^M_a}=a. Nierówność w nawiasie powyższego wzoru określa dwustronny obszar krytyczny testu, czyli gdy przy porównaniu wartości u wyznaczonej ?e wzoru z wartością u_a odczytaną z tablicy zajdzie nierówność \u\^u_a, to sprawdzaną hipotezę H₀ odrzucamy na korzyść jej alternatywy H_l. Gdy zaś otrzymamy nierówność przeciwną, tj \u\<u_a> to nie ma podstaw do odrzucenia hipotezy H₀

Uwaga. .Dla hipotezy alternatywnej H_x: m_x<m₂ stosujemy test istotności z lewostronnym obszarem krytycznym U^u_a Wartość krytyczną //* odczytuje się wtedy z tablicy rozkładu N(0, 1) tak, by P{U^u_a}=a Natomiast dla hipotezy alternatywnej H_x : m_x>m₂ stosujemy test z prawostronnym obszarem krytycznym U^u_a. Wartość krytyczną u_a odczy tuje się wtedy z tablicy rozkładu N(0, 1) tak, by zachodziło P {U^-u_a}=a

Model II. Badamy dwie populacje generalne mające rozkłady normalne N(m_x, a_x) oraz Ń(m₂₎ cr₂), przy czym odchylenia standardowe tych po pulacji są nieznane, ale jednakowe, tzn. zachodzi c_x=a₂ Na podstawie wyników dwu małych prób odpowiednio o liczebnościąch n_x f n^. wy losowanych niezależnie z tych populacji, należy zweryfikować hipotezę H₀ : m_x=m₂ wobec hipotezy alternatywnej m_x (i Greń