86 (64)

Matematyka. Zbiór zadań do liceów i techników. Klasa III

*7.261 . W każdej z dwu urn jest 5 kul białych, 10 czerwonych i 6 zielonych. Losujemy po jednej kuli z każdej urny. Oblicz prawdopodobieństwo, że obie wylosowane kule są tego samego koloru.

*7.262. W każdej z dwóch urn jest n kul białych i 3 czarne. Z każdej urny losujemy po jednej kuli i wkładamy je do trzeciej urny, początkowo pustej, a następnie losujemy z tej urny jedną kulę. Wyznacz najmniejsze /z, przy którym prawdopodobieństwo wylosowania kuli białej jest większe

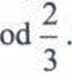
*7.263. W każdej z dwóch urn jest n razy więcej kul białych niż czarnych. Losujemy po jednej kuli z każdej urny i wkładamy je do trzeciej urny, początkowo pustej, a następnie losujemy z tej urny jedną kulę. Wyznacz najmniejsze /z, przy którym prawdopodobieństwo wylosowania kuli

białej jest większe od ^.

*7.264. W pierwszej umie jest dwa razy więcej kul białych niż czarnych, natomiast w drugiej . umie trzy razy więcej kul czarnych niż białych. Z każdej z tych um losujemy po jednej kuli, a następnie z tych dwu kul losujemy jedną. Oblicz prawdopodobieństwo, że będzie to kula biała.

*7.265. W pierwszej umie są 2 białe i 4 czarne kule, w drugiej zaś 4 białe i 2 czarne. Rzucamy kostką do gry. Jeżeli wypadnie liczba nieparzysta, to losujemy z każdej urny po jednej kuli, jeśli zaś parzysta, to losujemy jednocześnie dwie kule z pierwszej urny. Oblicz prawdopodobieństwo wylosowania dwóch kul o różnych kolorach.

*7.266 . W każdej z trzech um znajduje się n kul białych i n kul czarnych. Z każdej urny losujemy jedną kulę, a następnie z tych trzech wylosowanych kul losujemy jedną kulę. Oblicz prawdopodobieństwo, że będzie to kula biała.

**7.267. Strzelec oddaje n niezależnych strzałów do celu, przy czym prawdopodobieństwo chybienia do celu w k-tym strzale wynosi--— (A: = 1,2,..., ń). Wykaż, że prawdopodobieństwo

(¹+o²

w + 2

trafienia we wszystkich n strzałach wynosi-.

2(,i + l)

*7.268. Z trzech osób A>B\C może na wycieczkę pojechać tylko jedna osoba. Osoby te rzucają kolejno monetą: najpierw osoba A, potem B, potem C, potem znów A itd. Na wycieczkę pojedzie ta osoba, która pierwsza wyrzuci orła. Czy przy tej metodzie wszystkie osoby mają jednakową szansę na wyjazd? Odpowiedź uzasadnij.

Schemat Bernoulliego

86

1

7.269. Oblicz prawdopodobieństwo, że w dziesięciu rzutach monetą otrzymamy: a) dwa razy orła,    b) przynajmniej raz orła, c) co najwyżej raz orła.