HPIM0793

4.

4.2. Kinematyka robotów o strukturze szeregowej

tfmoł*v przypadWc odwzorowywania układów

_unj^ic i obrót określające pozycję punktu P w układzie {P} względem układu {i! zilustrowano na rys. 4.9.

%

twii:

***** ^{Bl    układu [A\

OfajOKtyjr'* obrotu ufchdł n^pókzęchwh

Qpg nbm \vi§M«tt ukbdu [B\ jest many. szukany zaś jest opis względem ufrfrfr cy^-kS. Oznaczmy: ^SP - opis wektora P względem układu {B)_% >-<ęewektcoP\\zgMcm układu J.4J

1 ft

1F& I

_;_

Ops Ktaao ^ff »-agłęiqa oferocooego układu współrzędnych

Wektor 'P względem obróconego układu współrzędnych opisuje się za po-mccą składowych ‘P- Składowe wektora ^łP odpowiadają rzutom wektora ^BP na osie współrEędn>xh układu J.ł}. Składowe te znajduje się z iloczynu skalarnego

(4.11)

(4.12)

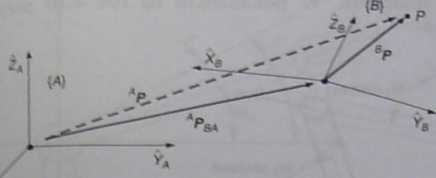
RyMncfc 4.9 _______

Przesunięcie i obrót określające pozycję punktu P wr układzie {£} względem układu {.4}

0910212008 A4 A7

Ogólne przekształcenie odwzorowujące opis wektora względem jednego układu w opis względem drugiego układu, uwzględniając przesunięcie między początkami układów współrzędnych, określa wzór

(4.13)

4.2.3.    Transformacja prosta ramienia o dwóch stopniach swobody

Dla dwuwymiarowego robota o dwóch stopniach swobody pokazanego na rys. 4.5 można ustalić pozycję końca efektora w przestrzeni, definiując wektory dla ramienia /| i dla ramienia /j

ri = [/icos^u /|SinĆ?₍]    (4.14)

r> = [/2C0S(^1 + Ą), /₂sin(<9i +    (4.15)

Po dodaniu wektorów (4.14) i (4.15) otrzymuje się współrzędne .r. r końca efektora w przestrzeni

.V = /icos^i +/2Cos(^i + Ą)    (4.16)

| = ł\sin&i + /2sin(d| + Ą)    (4.17)

4.2.4.    Transformacja odwrotna ramienia o dwóch stopniach swobody

W wielu przypadkach jest znacznie ważniejsze, aby znając kąty obrotu w dwóch przegubach, znaleźć położenie końca ramienia w przestrzeni. Typowa sytuacja występuje wówczas, gdy operator musi policzyć te kąty. aby przesunąć efektor do punktu w przestrzeni zdefiniowanego przez jego współrzędne. Dla robota 95