140

278 XXII. Badanie przebiegu zmienności funkcji

Układamy tabelkę przebiegu zmienności funkcji:

X	— 00	...		0	...	1		+ oo
y"	0	-	0	+ co	+	+	+	0
y	i	+	0	— 00	-	0	+	1
y	— 00	y	0	+ 0O	\	e	y	+ 00

Wykres funkcji podaje rysunek 13.7.

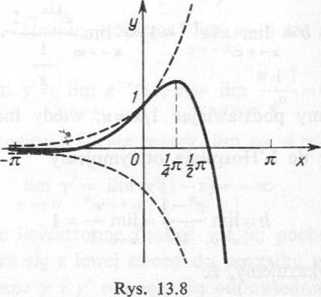
Zadanie 13.8. Zbadać przebieg zmienności funkcji _y=e*cos a.

Rozwiązanie. Funkcja jest określona dla wszystkich x. Ponieważ cos* przybi_er wartości zawarte pomiędzy -lii, więc funkcja y = e^x cos * jest krzywą oscylującą _po między liniami y— — e^x i y = e^x.

Badamy pochodną

y = e*(cos * — sin *).

Mamy y' = 0, gdy x = ^K + kn, gdzie k jest dowolną liczbą całkowitą.

Obliczamy drugą pochodną:

y" = — 2e^x sin x .

Mamy y"-0, gdy sin* = 0.

Gdy x = (2k +1) 7t, to funkcje e^x cos * i —e^x są równe, a także pochodne tych funkcji są równe: e*(cos * — sin x) = — e^x, a więc dowodzi to, że krzywe y = e^x cos x i y= -e są w tych punktach styczne. Gdy x = 2kn, to funkcje e^x cos x i e^x, a także pochodne tych

. A

funkcji są równe: e*(cos *—sin x) — e^x, co dowodzi, że krzywe y=e^x cos x i y w tych punktach styczne.    .

Zauważmy jeszcze, że w punktach styczności krzywej y = e^x cos x z krzywy^ml ? ^ i y — —_e^x druga pochodna funkcji y — e^x cos * staje się równa zeru, zmieniając J

. znak, co dowodzi, że te punkty styczności są jednocześnie punktami przegięcia

rLs«**-

rLy _x-»-oo, to y->0, a więc oś Ox jest jednostronną asymptotą poziomą krzywej. Układamy tabelkę przebiegu zmienności funkcji y = e^x cos x (w przedziale 0<x^27t)

X L-— f	...	0	...	i^n		i*		TC	...	!*		!*	...	In	...
	...	0	-	-	-	-	-	0	+	+	+	+	+	0
V		1	+	0	-	-	-	-	-	0	+	+	+	<■’*
r		1	/	M	\	0	\	—e^n	\	m	/	0	/	e^2lt

Wykres funkcji przedstawia rysunek 13.8.

Zadanie 13.9. Zbadać przebieg zmienności i podać szkic wykresu funkcji

'=K)‘

Rozwiązanie. Funkcja jest ciągła, gdy l + l/x>0, czyli gdy (x+l)/x>0, a więc dlax< -1 albo x>0. Nie należy stąd wnioskować, że funkcja jest nieokreślona dla wszystkich punktów przedziału — loc<0; tak np. dla jc= —§ mamy

/(-i)=(-!r^ł=37=L v(-₅)

tatwo wykazać, że dla liczb postaci x = -k/(2n+ lj, gdzie k i n są liczbami naturalnymi, Prcy czym k < 2n +1, rozpatrywana funkcja jest określona; natomiast dla liczb postaci ^x'~{2k-l)j2n, kin — naturalne, 2 k— 1 <2n funkcja nie jest określona. A więc funkcja ^ i^est ciągła w przedziale — 1 < jc < 0.

Przedstawmy funkcję w postaci wykładniczej:

x ln(l+ i )

y = e ^v *

^iczmy jej pochodną

>Wⁿ(¹⁺;)

K*4h^4)K‘4rM4)^J-

X

^szy ezynnik jest dodatni. Rozpatrzmy znak drugiego czynnika

z-lnfi+1)--—,

V x) x+l