1tom043

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 88

Tablica 3.1 (cd.)

Ciała nieswobodne Schematy

walcowy (niektóre łożyska, zawiasy)

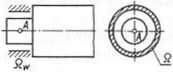
kulisty ruchomy

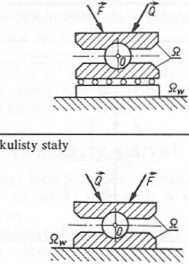
Utwierdzenie

Ciała swobodne (uwolnione od więzów) Schematy

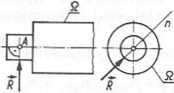
X /

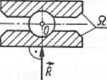
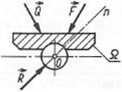
stałe przesuwne

1

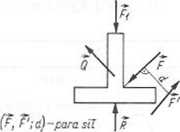
całkowite

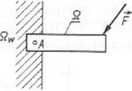
p/ (f, P;d)~paro sil

A - środek utwierdzenia

Oznaczenia: Q _ ciało nieswobodne sztywne, Q_w — więzy, / prosta o znanym kierunku, n — prosta o nie znanym kierunku, R — reakcje więzów', G - siła ciężkości, q — siła jednostkowa.

3.2.4. Wypadkowa dwóch sił

Niech na ciało sztywne działają w jednej płaszczyźnie dwie siły F_l i F₂, których suma F_r^Ą+F₂.

Rozpatruje się następujące przypadki:

1 Kąt między siłami oe <0jc>; proste działania sił mają co najmniej jeden punkt wspólny. Wypadkowa F_r = F_l + F₂ działa wzdłuż przekątnej równoległoboku zbudowanego na tych siłach (rys. 3.1), gdy ae(0, n) lub działa wzdłuż prostych działania sił F„ F₂, gdy ae{0, Jt}.

Jej wartość wylicza się ze wzoru

F,=«

_N/Ff+2f, F₂ cos a + F 2 F_t + F₂

f₁-f₂

f₂-f,

gdy ae(0, iz) gdy a = 0 gdy a = n, F_l gdy a = w, F₂

(3.1)

>f.

2. Siły równoległego zgodnych zwrotach (rys. 3.2).

Wypadkowa F, = F₁ + F₂ działa wzdłuż, prostej prostopadłej do odcinka AB w punkcie D znajdującego się w odległości wyznaczonej z równania

(3.2)

(3.3)

F, BP J~₂ ~ AD a jej wartość F, = F_i+F₂

3. Siły równoległe o przeciwnych zwrotach (rys. 3.3).

Rys. 3.2. Wypadkowa dwóch sił równoległych o tych samych zwrotach konstrukcja

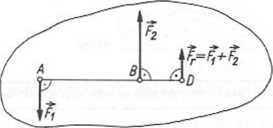
Rys. 3.3. Wypadkowa dwóch sił równoległych o przeciwnych zwrotach

Wypadkowa F_r = F_l + F₂ działa wzdłuż prostej prostopadłej do odcinka A B w punkcie D, usytuowanego w odległości obliczonej z zależności

(3.4)

(3.5)

fj__ BD

F₂~~AD a jej wartość

F_r=Fl__F

[F₂-F„ gdy F₂>F,

We wzorach: F,, F₂, F_r — siła, N; AD, BD — długość odcinka, m.