1tom051

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 104

Właściwości:

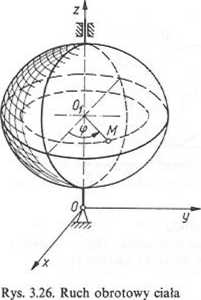
1.    Torem dowolnego punktu MeQ jest okrąg leżący w płaszczyźnie prostopadłej do osi obrotu przechodzącej przez M o promieniu r_M = O_lM (rys. 3.26).

2.    Prędkości i przyspieszenia punktów ciała (2, leżących w płaszczyźnie prostopadłej do osi obrotu, są liniowymi funkcjami odległości tych punktów od osi obrotu; oblicza się je ze wzorów (3.26...3.29).

Równanie kinematyczne

<P =f(t)    (3.33)

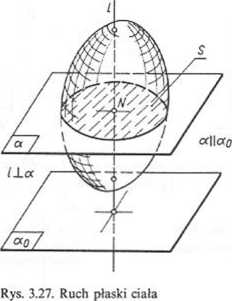
Ruch plaski. Ciało Q jest w ruchu płaskim, jeżeli jego punkty poruszają się w płaszczyznach równoległych do pewnej stałej płaszczyzny zwanej płaszczyzną prowadzącą a₀ (rys. 3.27). Właściwości

1.    Prosta przechodząca przez dowolny punkt N e Q prostopadła do a₀ porusza się ruchem postępowym.

2.    Część wspólna (iloczyn mnogościowy) ciała (zbioru) Q i dowolnej płaszczyzny (zbioru) a||a₀ w pełni określa ruch ciała Q. Iloczyn Qrvx = S jest nazywany figurą płaską (rys. 3.27).

3.    Ruch plaski jest złożeniem ruchu postępowego bieguna i ruchu obrotowego wokół tego bieguna.

4.    Istnieje punkt figury płaskiej (płaszczyzny sztywno związanej z figurą płaską), którego prędkość w danej chwili jest równa zeru; punkt ten jest nazywany chwilowym środkiem prędkości.

5.    Ruch figury płaskiej jest ruchem obrotowym względem chwilowego środka obrotu, który pokrywa się z chwilowym środkiem prędkości.

Równanie kinematyczne

=/,(t);    y a =/₂(t);    <p =m    (3.34)

w którym: x_A, y_A — współrzędne bieguna A; Ap — półprosta stale równoległa do osi Ox (rys. 3.28), <p = %(AM, Ap), M — dowolny punkt S — Q a a.

Twierdzenie: Prędkość dowolnego punktu figury płaskiej jest równa sumie prędkości bieguna i prędkości tego punktu wokół bieguna (rys. 3.38), a wiec

=~Ć_A +7_Am    ~»am = 3x AM    (3.35)

(JO —

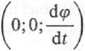
nie zależy od wyboru bieguna.

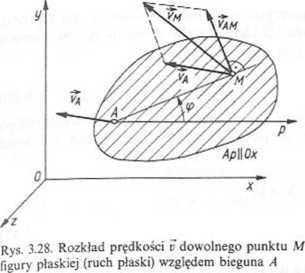
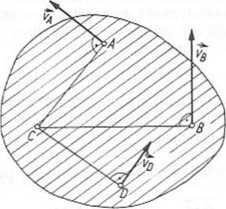
Rys. 3.29. Prędkości punktów figury płaskiej (ruch płaski) względem chwilowego środka obrotu C jako bieguna

(v_c = 0)

Wniosek: Jeżeli biegunem jest chwilowy środek prędkości (obrotu), to prędkość dowol-nego punktu figury płaskiej jest równa prędkości tego punktu względem bieguna (rys. 3.29). Niech punkt C będzie chwilowym środkiem prędkości. Wówczas

^VA ~ ^V CA	vb = Vcb vd = vcd itd-				(3.36)
Stąd, i ze wzoru	(3.27), wartości prędkości	do>			(3.37)
vA = co-CA	vb = co-CB vd = co-CD itd.,	w = — di		►
lub — = —	= — itd.
CA CB	CD

Twierdzenie: Przyspieszenie dowolnego punktu figury płaskiej jest sumą przyspieszenia bieguna i przyspieszenia tego punktu wokół bieguna (rys. 3.30). A zatem

^aM — ^aA + ^aAM ^aAM ⁼ aiAM ^{+ a}nAM    (3.38)

a_zAM = ^-x AM a„_AM =5x(5x AM)    (3.39)

Ruch kulisty. Ciało O jest w ruchu kulistym, jeżeli istnieje jeden punkt ciała, którego prędkość jest równa zeru (rys. 3.31).

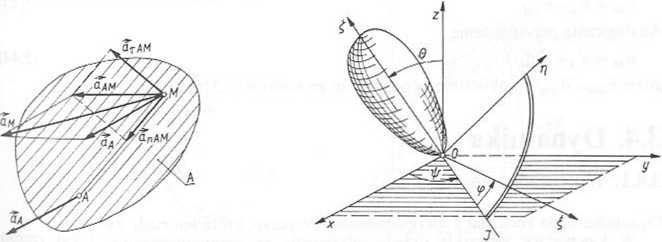
przyspieszenia a dowolnego P nktu M figury płaskiej (ruch płaski) wzglcdem ^bieguna A

Rys. 3.31. Ciało w ruchu kulistym J krawędź przecięcia płaszczyzn Oxy i Ot]Ę,