1tom055

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 112

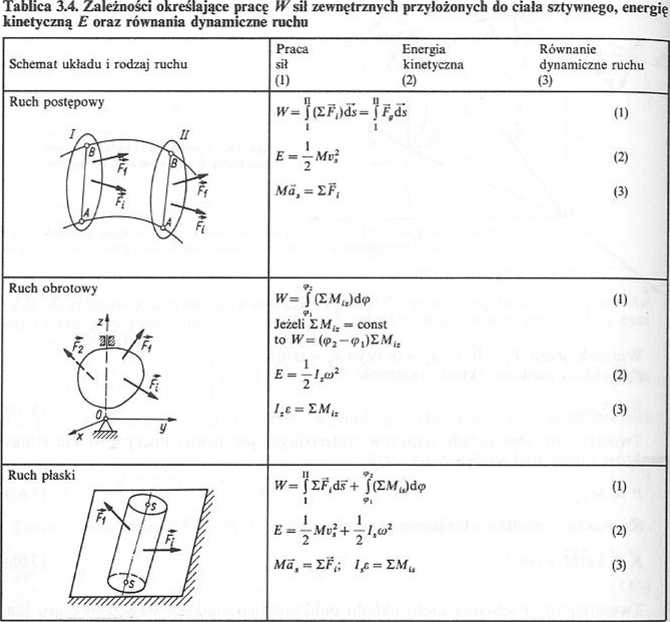
3.4.5. Zasada prac wirtualnych (przygotowanych)

Niech na układ nieswobodnych punktów materialnych    z,),M„(x„; _y„; z„) będą

nałożone stacjonarne dwustronne więzy

fj(x 1, y_t; zd y„; z„) = 0, j = 1    < n    (3.69)

Liczbę s = 3n—m nazywa się ilością stopni swobody układu punktów. Zbiór niezależnych parametrów q_vq_s opisujących ruch układu punktów materialnych określa się jako współrzędne uogólnione.

Z powyższego wynika, że

= x, {q_v...,    y, = y_t(q_t,..., qj j    _?0)

z,-=z,(«_l.-.g_J);    (i=l,..,») J

Na przykład współrzędne punktów A(x_a; y_A) i B(x_b; y_B) mechanizmu korbowego (rys. 3.43) spełniają równanie więzów

x²A+y²A = r²; y_B = 0

j są funkcjami współrzędnej uogólnionej <p postaci

_Xl = rcosę>; >;, = rsintp; x_B = rcoscp+^/l² — r²sin²ę>;    = 0

Przesunięciem wirtualnym (możliwym) nieswobodnego układu punktów materialnych jest nazywane wyobrażalne, dowolnie małe, prostoliniowe, skierowane przemieszczenie układu, na które w danej chwili pozwalają więzy nałożone na układ. Na przykład przemieszczeniem wirtualnym pręta AB (rys. 3.44) jest jego obrót o nieskończenie mały kąt 5ę> wokół punktu O, a przemieszczeniem wirtualnym punktów A i B są odpowiednio wektory: Ssj,, 8s_B. Ich wartości są równe: 6s,, = OAhtp, Ss_B = OBów.

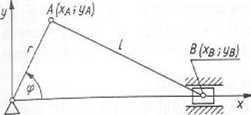
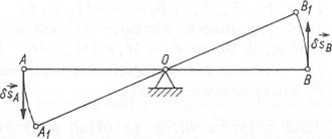
Rys. 3.43. Mechanizm korbowowodzikowy    Rys. 3.44. Przemieszczenie wirtualne (ilustracja)

— przykład więzów stacjonarnych

dwustronnych

Ze wzoru (3.70) przez zróżniczkowanie względem czasu, zastąpienie formalne róż-niczek dx,-, dy-„ dz₍ przez 6x_it §>,, 8z_f oraz przyjęcie: 8.x_t = x,z, 8y, = y.t, 8z_; = ż,t (t — parametr, i = l,...,n); 8q_s — q_;r, (J = l,...,s) otrzymano

i, dx_t

8x,.= £ -t-8^; ;= i ^vllj

Z zależności

8^=

;=i ^dcli

Sz; = I — §<?; J-lfy

(3.71)

Ssj = (8x,-; 8y,; 62,) = (x,t; y_fT; ż,z)

wynika, że przesunięcia przygotowane są proporcjonalnie do prędkości możliwych punktów materialnych.

Więzy_ określone zależnością (3.69) nazywa się idealnymi, jeżeli suma prac reakcji więzów R,-, (i = 1,...,n) przy dowolnym przesunięciu wirtualnym 8sj, (i = 1jest równa zeru, a zatem

SR,-87, = IR,8SjCos(R,, 8sj) = 0    (3.72)

Zasada prac wirtualnych: Warunkiem koniecznym i wystarczającym równowagi układu sil działających na układ punktów materialnych z_więząrni stacjonarnymi, dwustronnymi i idealnymi jest,_aby suma prac sił zadanych {F,,...,F„} przy dowolnym przemieszczeniu wirtualnym {87;,..., 8s„} układu punktów materialnych równała się zeru, a zatem

EFiSs,- = IF_i8.s_icos(R_i, 87J = 0    (3.73)

Dla więzów jednostronnych (w (3.69) znak = zastępuje się <)

87,. = SFjSijCos(Rj, 87,) < 0    (3.74)

, Ogólne równanie dynamiki: Niech będzie dany układ punktów materialnych ^M\(^xu y_}; z_t),..., iW_n(x„; y„; z„) z więzami dwustronnymi, stacjonarnymi, idealnymi opisanymi zależnością (3.69). Zatem na każdy punkt materialny M; o masie m_; działa siła zewnętrzna F_;, reakcja więzów R_; oraz siła bezwładności B,= —m^a^ czyli

fi + Rj+B. = 0, (i =!,...,«)

Poradnik inżyniera elektryka tom 1