1tom048

3. MECHANIKA TECHNICZNA 1 WYTRZYMAŁOŚĆ MATERIAŁÓW 98

Wypadkową R można obrócić wokół prostej działania siły N o kąt 2it. W ten sposób otrzymujej>ię stożek tarcia o wysokości N, tworzącej R i promieniu podstawy T. Kąt 8 = <(R;N) jest nazywany katem tarcia dlatego, że

T=N tgg czyli /i = tgq    (3.8)

Jeżeli współrzędna prędkości względnej ciał trących się jest większa od zera, to wtedy tarcie między ciałami nazywa się tarciem kinetycznym. W tym przypadku współczynnik tarcia H jest funkcją wartości u prędkości względnej u, a więc /i = f(u) a wartość siły tarcia

T= Nf(u)    (3.9)

Typowe przebiegi funkcji f(u) przedstawiono na rys. 3.16.

Rys. 3.16. Charakterystyki tarcia: a) opadająca; b) rosnąca; c) rosnąca, a następnie opadająca

W zagadnieniach praktycznych wygodnie jest posługiwać się tzw. charakterystyką tarcia, tj. funkcją, która jest nieparzystym przedłużeniem funkcji f(u). Zatem charakterystyka tarcia

/(«,), «_r > 0

-/(u_t), u, < 0

gdzie: u = u,x, t — wersor stycznej.

Współrzędna siły tarcia T względem osi o wersorze t jest równa 71 = Ncp(u_t), a więc wartość siły tarcia T = Nę(u_t).

3.2.10. Geometria mas

Rozkład mas w układzie punktów materialnych lub ciała ma istotny wpływ na ich ruch z wyjątkiem tylko ruchu postępowego. W celu scharakteryzowania rozkładu mas wprowadzono pewne pojęcia, których ujęcie analityczne podano dla ciała sztywnego. W przypadku punktów materialnych wystarczy znak całki zastąpić znakiem sumy.

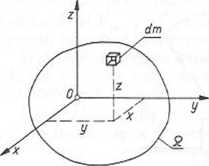
Rys. 3.17. Ilustracja geometryczna do obliczania momentów statycznych i momentów bezwładności ciała

Momenty statyczne względem płaszczyzn układu Oxy, Oyz, Ozx (rys. 3.17) — oznaczone odpowiednio S_xy, S_y,,S._x — określono w następujący sposób:

_a środek masy

(3.11)

S_xy = f z Am;    S_yz = J xdm;    S_zx =

J ydm

a

(3.10)

(x,;y,;zj = I/(j[^xdm;j/^dm:j[^zdm

przy czym: M = J dm;dm — elementarna masa, kg; x,y,z — współrzędne dm, m.

n

Momenty bezwładności względem osi 0x, Oy, Oz układu współrzędnych Oxyz (rys. 3.17), oznaczone odpowiednio I_x, I_y, a względem początku układu O —1₀, wyrażone w kg m², definiuje się w następujący sposób:

1₀ = J (x²+y²+z²)dm n

(3.12)

I_x = \(y²+z²)Am n

l_z = j(x²+y²)dm a

I_y = J (x² + z²) Am a

Stąd wynika

(3.13)

/₀ = —(I_x + I_y+I.)

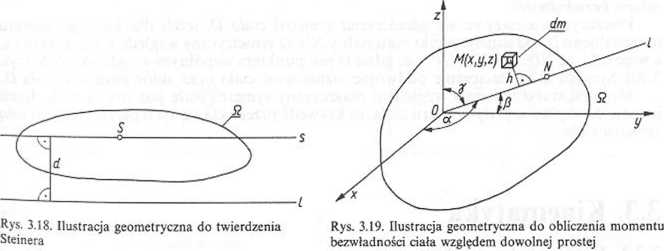
Twierdzenie Steinera: Moment bezwładności ciała Q względem prostej l równoległej do prostej s przechodzącej przez środek masy S ciała Q (rys. 3.18) wyraża się wzorem

!, = !, +Md²    (3.14)

gdzie: M — masa ciała Q, d — odległość między prostymi / i s.

Momenty dewiacji ciała Q względem osi x i y, y i r, z i x układu współrzędnych Oxyz (rys. 3.17) — oznaczone odpowiednio I_xy, I_y:, I._x — określa się w następujący sposób:

I_xy = f xyAm; I_yz = J yzdm; I._x = [ zxdm    (3.15)

o    n    n

Moment bezwładności ciała względem prostej dowolnej. Niech 0 będzie dowolnym Punktom ciała Q. W punkcie O umieszczono początek układu współrzędnych Oxyz (rys. 3-19). Położenie prostej / jest określone przez kąty a, (1, y. Moment bezwładności ciała “ względem prostej l wyraża się wzorem

^!i = I_x cos²ot+I_y cos²/?+I_z cos²y—2I_y, cos/?cosy—2I_zx cosycosa—2I_xy cosacos/? (3.16)

7*