1tom049

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 100

Równanie (3.16) można sprowadzić do postaci

I_xx²+I_yy²+I_Jz²—2I_yiyz—2I_zxzx—2I_xyxy = 1    (3.17)

przez podstawienie: cos²« = I,x², cos²/) = I,y², cos²y = /,z²; przy czym x, y, z są współrzędnymi punktu N (rys. 3.19). Współczynniki l_x, I_y, I_r równania (3.17) są wielkościami dodatnimi, natomiast 1,1, I_xy mogą być dodatnie, ujemne lub równe zeru. Obrazem geometrycznym równania (3.17)jest powierzchnia elipsoidy. Przez obrót układu współrzędnych wokół początku układu zależność (3.17) można doprowadzić do postaci

i    ir z

(V^)² (V*)² (Jćy

= i

(3.18)

gdzie: A, B, C — stałe dodatnie, zależne od momentów bezwładności I_x, I_y, I..

Równanie (3.18) jest równaniem elipsoidy bezwładności, a osie tej elipsoidy są głównymi osiami bezwładności.

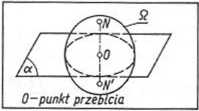
Rys. 3.20. Płaszczyzna symetrii ciała

Momenty dewiacji ciała względem osi układu współrzędnych, którego osie są głównymi osiami bezwładności (osie elipsoidy bezwładności) są równe zeru. Jeżeli osie układu współrzędnych są głównymi osiami bezwładności i początek układu znajduje się w środku masy ciała, to osie układu współrzędnych nazywa się głównymi, centralnymi osiami bezwładności.

Płaszczyznę a nazywa się płaszczyzną symetrii ciała O, jeżeli dla każdego punktu materialnego N e Q istnieje punkt materialny N' e Q symetryczny względem płaszczyzny a, a więc taki, że NO — ON', NN' 1 a, gdzie O jest punktem wspólnym a i odcinka NN' (rys. 3.20). Symbol Q ma znaczenie podwójne: oznaczenie ciała oraz zbiór punktów ciała Q.

Moment statyczny ciała względem płaszczyzny symetrii ciała jest równy zeru. Jeżeli istnieją dwie płaszczyzny symetrii ciała, to krawędź przecięcia się tych płaszczyzn jest osią symetrii ciała.

3.3. Kinematyka

3.3.1. Kinematyka punktu

Kinematyka jest to geometria ruchu punktów materialnych i ciał sztywnych.

Tor punktu jest to miejsce geometryczne kolejnych położeń punktu w przestrzeni. Opisuje się go analitycznie jako krawędź przecięcia się dwóch powierzchni Sj(x;y;z) = 0, S₂(x;y;z) = 0 lub za pomocą równań parametrycznych: x = /j(t);y = /₂(t); z =/₃(t), gdzie t oznacza czas.

Ruch punktu można opisać w sposób:

—    naturalny — podając tor punktu i sposób poruszania się punktu po torze, tj. współrzędną łukową;

—    wektorowy — podając wektor położenia punktu;

—    równaniami skończonymi — podając współrzędne punktu w zorientowanej przestrzeni. Ważnym pojęciem w kinematyce jest pojęcie prędkości i przyspieszenia punktu. Znając

wektor położenia punktu T(t) prędkość można zdefiniować

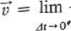
oraz przyspieszenie

F(l + At)—r(t)

(3.19)

przy czym zakłada się, że granice te istnieją.

Analityczne przedstawienie sposobów opisu ruchu punktu

W tym celu wprowadzono oznaczenia: a—droga przebyta przez punkt M w czasie od t₀ do t,,m;s = 0₁M — współrzędna łukowa mierzona po torze od stałego punktu O,, m (rys. 3.21); F = OM — wektor położenia punktu M (rys. 3.21); (x,y,z) — współrzędne punktu M, m (rys. 3.21); q — promień krzywizny toru; t ■—czas, s; F—prędkość punktu M, m/s; a — przyspieszenie punktu M, m/s².    __    _    _    _    ___

Sposób wektorowy. Dany jest wektor położenia r = xi +yj +zk, wersory i,j,k są stałe (rys. 3.21). Wówczas

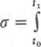
(3.21)

_ dr

i; = — = xi +yj +zk

_ dF

a = —— = xi +yj +zk ćt

przy czym: x,y,ż — pochodne funkcji względem czasu; x, y, z—pochodne rzędu drugiego funkcji względem czasu.

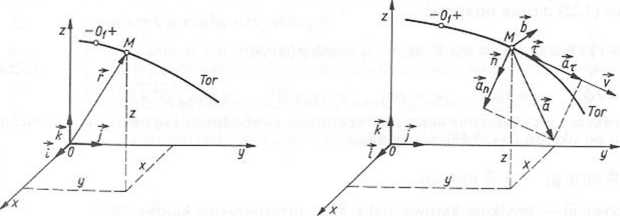
Rys. 3.2!. Ilustracja geometryczna do opisu ruchu punktu

Rys. 3.22. Położenie prędkości v punktu względem toru i rozkład przyspieszenia a punktu

Sposób naturalny. Dana jest współrzędna łukowa O_lM — s(t) (rys. 3.21). W tym przypadku wygodnie jest prędkość i przyspieszenie przedstawić w ruchomym układzie współrzędnych Mznb o początku w punkcie M i wersorach osi z, n, b = r x n (rys. 3.22), przy czym wersory te są odpowiednio wersorami stycznej, normalnej i binormalnej do toru w punkcie M. Zatem

przy czym <r = sjtj)—s(l₀), gdy — >0