1tom053

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 108

mx = I.F_lx; my = XF_iy; mż = ZF_iz    (3.48)

gdzie: a = (x; j>;z); F_i = (F _ix; F ■; F _i:).

Natomiast w układzie współrzędnych Mtnb (rys. 3.37)

d²s

dr^:

= 2f_ir;

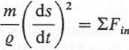
(3.49)

gdzie: F, = (F_it; F_in;0); ZF_ib = 0;s — współrzędna łukowa; q — promień krzywizny toru punktu M.

Pierwsze zadanie dynamiki. Dana jest masa m punktu materialnego oraz równania jego ruchu: x =/,(t), y =/₂(t), z = /₃(t) w stałym układzie współrzędnych Oxyz. Znaleźć siłę F działającą na ten punkt.

Rozwiązanie. Uwzględniając równania (3.48) siła

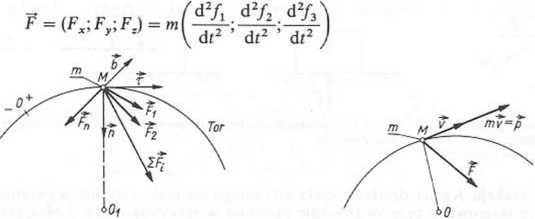
Rys. 3.37. Ruch punktu materialnego pod działaniem Rys. 3.38. Pęd punktu materialnego (ilustracja) sił w naturalnym (ruchomym) układzie M

(3.50)

Drugie zadanie dynamiki. Dana jest masa m punktu, siły działające na ten punkt {F_Ł,...,/•'„} oraz warunki początkowe (x(0);y(0);z(0)) = (x₀;y₀;z₀)

(x(0);y(0);ż(0)) = (x₀;y₀;ż„)

gdzie: x, y, z — współrzędne punktu materialnego w Oxyz Fj = (^Fix'>Fj,',Fjz) (j=

Rozwiązanie. Uwzględniając równania (3.48) otrzymuje się tzw. problem początkowy

x = - ZF_ix; y = — ZF_f,; ż = — ZF_ix m    m    m

^(0) = x₀;    y(0) = y₀;    z(0) = z₀

J6(0) = x₀;    y(0) = y₀;    ż(0) = ż₀

W ogólnym przypadku Fj = ęj(x;y; z; x;y;ż;t); przy pewnych założeniach o funkcjach <p_; istnieje jedno rozwiązanie tego problemu początkowego, które można zapisać

(3.51)

(3.52)

* ^f\{x₀,y₀,z₀,x₀,y₀,ż₀,t) y=f2(x₀,y₀,z₀,x₀,y₀,ż₀,t)

² =Mx₀,y₀,z₀,x₀,y₀,ż₀,t)

/

Pędem punktu o masie m i prędkości TT (rys. 3.38) jest nazywany iloczyn niv — p

Popędem siły F działającej na punkt materialny w przedziale czasu od t₂ do t, jest nazywany wektor

'\Fdt = n    (3.53)

f,

Jeżeli F = const, to 77 = F(t₂ — z,).

Zasada pędu i popędu: Przyrost pędu punktu w czasie jest równy popędowi siły w tym czasie, a zatem

P(f₂)-P(ł i) = n    (3.54)

Wniosek: jeżeli /7 = 0, to p = const.

Moment pędu (kręt)jest to iloczyn wektorowy wektora położenia OM punktu M i pędu p (rys. 3.38), a więc

k₀ = OM x p = OM x(mb)    (3.55)

Twierdzenie o zmianie krętu: Pochodna krętu względem czasu jest równa momentowi siły

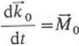
lub

(3.56)

(M_x; M_y; M_z)

dk* d k_y dk₂ \

d£ ’ d£ ’ dt J

przy czym kręt i moment siły są obliczone względem tego samego punktu. Wniosek: Jeżeli M₀ = Ó", to k₀ = const; jeżeli np.: M_x = 0, to k_x = const.

3.4.3. Zasada równoważności energii kinetycznej i pracy, zasada zachowania energii

Jeżeli każdemu punktowi zbioru Q przyporządkuje się siłę, to oznacza, że w Q jest określone pole sił.

^y77///^/>/77//7//7///77/ĄV////

Rys. 3.39. Praca stałej siły na prostoliniowym przemieszczeniu (ilustracja)

Pracą stałej siły F przyłożonej do punktu materialnego na prostoliniowym przesunięciu AB (rys. 3.39) jest nazywany iloczyn skalamy

W=P-AŚ=F-AB cosa ae<0,tt>    (3.57)

Praca po krzywej k (rys. 3.40) zanurzonej w polu sił F = (P,Q,R) wyraża się za pomocą całki krzywoliniowej

Wi = jF-ds = SPdx+Qdy+Rdz, (F = F(x,y,z))    (3.58)

k    k

Pole sił jest polem potencjalnym, jeżeli praca po dowolnej krzywej zamkniętej jest równa zeru.

Praca sił pola ziemskiego F=(0;0;—mg) od punktu A(x₁;y_l;z_i) do punktu na rys. 3.41 wynosi fV= mg(z₂ — z₁).