1tom045

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 92

W wyniku redukcji otrzymuje się wypadkową F_r = £F, zaczepioną w punkcie O. Na rysunku 3.4 jest pokazana ta czynność dla n_= 4. Sumowania sil można dokonać poza ciałem (rys. 3.5b), następnie sumę sił F = ZF, można przesunąć równolegle do punktu O (rys. 3.5a).

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 92

b)

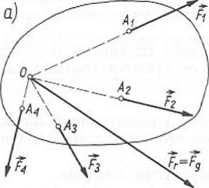
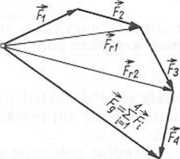
Rys. 3.5. Wektor główny jako: a) wypadkowa środkowego układu sił; b) suma sił w wiełoboku sił

Środkowy układ sił jest w równowadze, jeżeli wypadkowa sił jest równa zeru (jest wektorem zerowym). Także odwrotnie: jeżeli wypadkowa sił jest wektorem zerowym, to środkowy układ sił jest w równowadze. W przypadku trzech sił, siły te są w równowadze wtedy i tylko wtedy, gdy ich proste działania przecinają się w jednym punkcie i trójkąt sił jest trójkątem zamkniętym.

Dowolny układ sił

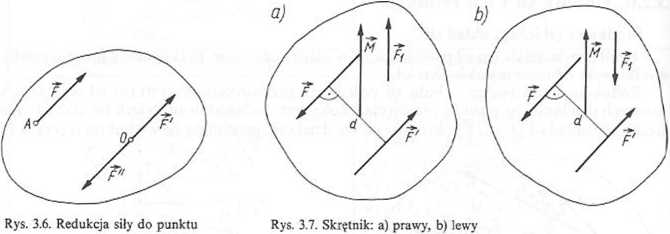
Niech w punkcie A ciała będzie zaczepiona siła F. W obrębie ciała obrano punkt O. Redukcja siły_F do punktu O polega na przyłożeniu w punkcie O odpowiedniej dwójki zerowej, tj. {(F', F");_F'||F;_F =_F'}. W_wyniku tej konstrukcji otrzymuje się parę sił (F, F"; d) o momencie M= OAxF i siłę F' zaczepioną w punkcie O (rysę 3.6).

Układ sił złożony z pary sił {(F, F'; d)} o momencie M oraz siły F, prostopadłej do płaszczyzny pary tych sił jest nazywany skrętnikiem. Rozróżnia się dwa rodzaje skrętników: jkrętnik prawy, jeżeli < (M; FJ = 0 (rys. 3.7a) oraz skrętnik lewy, jeżeli ł (M; Fj) = tt (rys. 3.7b).

Niech na ciało działa układ sił {F_v..., F„} i niech Aj będzie punktem zaczepienia siły Fj< a punkt O dowolnym punktem ciała. Oznaczono: F_g = 2F_; — wektor główny (wektor swobodny) oraz M_q = ’ZOA_jxFj — moment główny (wektor swobodny). Redukcja dowolnego układu sił polega na zredukowaniu wszystkich sił do_punktu O, tj. przyłożeniu w punkcie O ciała n odpowiednich dwójek zerowych: {(Fj, F"); Fj||Fj; Fj = F)}. W wyniku tej konstrukcji otrzymuje się środkowy układ sil {Fj,..., F'„} o środku w punkcie O, który zastępuje się silą F„ = F_g oraz układem par sił {(F), F'j; dj)}. Siły te następnie zastępuje się oara sił o momencie M = M_g. Na rysunku 3.8 przedstawiono ideę redukcji trzech sił.

Tak więc dowolny układ sił redukuje się do siły F₀ = F_g (przy czym_ F_g — wektor główny) zaczepionej w biegunie redukcji O i do pary sił o momencie M = M_g Jeżącej _w dowolnej płaszczyźnie (w obrębie ciała) prostopadłej do momentu głównego M_g.

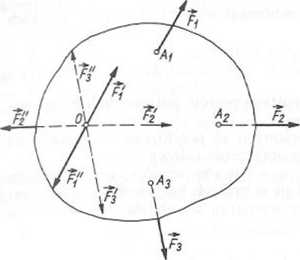
Rys. 3.8. Redukcja dowolnego układu sił. na przykładzie trzech sił

Tablica 33. Analityczne warunki równowagi sił przyłożonych do ciała sztywnego

Schemat układu

Układ sił

Warunki równowagi

płaski

IX, = o, iy_t = o F, = (X,; Y_it0)

prze

strzenny

IX, = 0; IV, = 0; IZ, = 0 F,^(X_t;Y_i;Z_i)

IX, = 0; zy;. = 0; ZM_z(F„A) = 0

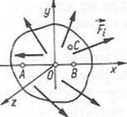
płaski

prze

strzenny

IX, = 0; IM_t(F„A) = O, M_i{F„B) = 0

oś Ox nie prostopadła do AB; A, B leżą na płaszczyźnie Oxy

IM_g{F,, A) = 0; IM_t(F„ B) = 0

ZM.(F„ Q = 0; A,B,C nie leżą na jednej prostej; leżą na płaszczyźnie Oxy F, = {X,; y;-;0)

IX, = 0; IY_t = 0; IZ, = 0

IMJF,) = O, IM_y(F,) = 0; ZM.(F,) = 0

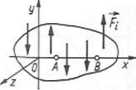
		ZY,= 0; £Ms(F„/4) = 0
	płaski	IM.(F,% A) = 0; IMt(F,, B) = 0
		/lB^O> ;/ł, B leżą w płaszczyźnie Oxy
-O		F, = (0; y;;0)
	prze-	11^ = 0; IM x(Fj) = O, ZM.(F,) = 0
	strzenny	Fj = (0; Y,;0)

Oznaczenia: M.(F_|;/1) współrzędna (względem osi Oz) momentu siły F, względem bieguna A, itd.; M_X{F,) - współrzędna (względem osi Ox) momentu siły F, względem osi Ox, itd., tj. współrzędna względem osi Ox momentu rzutu F_iyz, siły F, na płaszczyznę Oyz względem początku układu O, czyli M_x(F_iys, 0) — M_X(F,).