1tom054

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 110

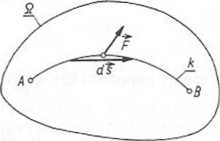
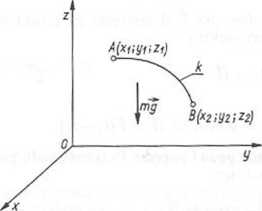
Rys. 3.40. Ilustracja geometryczna do pracy sił pola przy Rys. 3.41. Praca sił ziemskiego pola ruchu punktu po krzywej k (suma prac elementarnych) grawitacyjnego (ilustracja)

Zasada równoważności energii kinetycznej i pracy: Przyrost energii kinetycznej punktu materialnego przy przesunięciu od punktu A do punktu B jest równy pracy sit na tym przesunięciu. A zatem

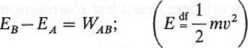
Potencjałem pola sił F = (P;Q;R) nazywa się funkcję skalarną ę(x,y,z) (jeżeli istnieje) taką, że

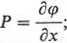
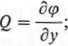
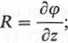
(3.60)

Twierdzenie: Pole sił F = (P; Q; R) jest polem sił potencjalnych wtedy i tylko wtedy,

gdy

8P_ ₌    dQ ₌ ÓR    dP_ ₌ 3R

dy    Sx ’ 8z dy’    dz    8x

Energia potencjalna E_v = — ip(x; y, z).

Zasada zachowania energii: W potencjalnym polu sił suma energii kinetycznej i potencjalnej jest stała, czyli E+E_v = const.

3.4.4. Dynamika układu punktów materialnych

Rozważmy układ n punktów materialnych M,(x,; y,; zj,..., M„{x„; y„; z„) przedstawiony na rys. 3.42. Oznaczenia: m_; — masa punktu M_f; F_t — suma sił zewnętrznych przyłożonych do M{, R_; — suma sił wewnętrznych przyłożonych do M;, S(x^ y_s; z_s) — środek masy punktów materialnych.

Równanie ruchu i-tego punktu ma postać

= F,+R i (i = 1,n)    (3.62)

Zasada ruchu środka masy: Środek masy układu punktów materialnych porusza się jak swobodny punkt materialny, o masie równej sumie mas wszystkich punktów, pod działaniem siły równej sumie sił zewnętrznych, a zatem

(3.63)

Ma, = F_g

gdzie: M = Zą-; F_g = £F₍; ER_f = 0.

Rys. 3.42. Nieswobodny układ punktów materialnych po uwolnieniu od więzów

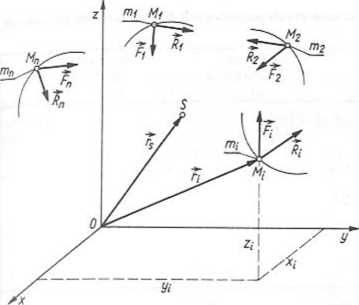
Wniosek: jeżeli F_g = 0, to a_s = 0, czyli v_s = const.

Pęd układu punktów określa zależność

P lim, o,    (3.64)

Twierdzenie: Pęd układu punktów materialnych jest równy iloczynowi sumy mas punktów i prędkości środka masy, czyli

P = Mv_s    (3.65)

Kręt układu punktów określa się ze wzoru

K = I OM, x (muj)    (3.66)

Twierdzenie: Pochodna krętu układu punktów materialnych względem czasu jest równa sumie momentów sił zewnętrznych, przy czym moment i kręt są obliczone

względem stałego, tego samego punktu (rys. 3.42), tj. K₀ = M lub w formie równoważnej

w Oxyz

dd K\ dt ’ dt ’ dt /

= (M_x; M_y; M.)

(3.67)

bo ZOA_ixR_i = 0.

i ^3 ą³?*³ r®^wnowa^^no*^c' ^energ" kinetycznej i pracy: Dla układu punktów materialnych

W"_A,_Bi    (3.68)

gdzie: E_Bi — energia kinetyczna punktu M, w położeniu Bp, E_Al — energia kinetyczna Punktu M,■ w położeniu A,-; W'_AtBl — praca siły zewnętrznej F, przyłożonej do punktu M_f ^przy przemieszczeniu po krzywej k_; od punktu A- do Bp W_AlBl— praca siły wewnętrznej R , P^ytożonej do M, przy przemieszczeniu po krzywej k_i od A_i do B_t.

W przypadku ciała sztywnego wc wzorze (3.68) ostatni składnik po prawej stronie jest równy zeru.

n, ,f°dstawowe wzory określające pracę, energie kinetyczną oraz równania dynamiczne ruchu podano w tabl. 3.4.