1tom059

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 120

jctórej: H— funkcja Heaviside’a, tj. H(x—x_r) =1 dla x > x_r oraz H(x—x_r) - 0 dla x < x_r; F; = (0:f!y0) — siła skupiona zaczepiona w punkcie a,-; Mj = (0; 0 ;M_j2)—moment " ary sit przyłożonej w punkcie by q_s = (0; q_y; 0) — obciążenie ciągłe, stałe, q_sy t⁴ 0 dla v6<c , c,,,); obciążenie belki jest w płaszczyźnie Oxy układu Oxyz.

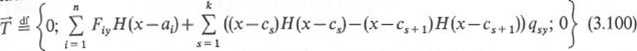
Silą poprzeczną T(x) w przekroju poprzecznym belki w punkcie x nazywa się wektor postaci

dla x t⁴ by, w punkcie x = bj należy obliczyć granicę lewo- i prawostronną (j = 1,..., m).

^(x-0)²/f(x-0)

przykład. Wyznaczyć moment gnący dla belki (rys. 3.51 b) obciążonej parą sił o momencie M = (0; 0;—M) w punkcie a silą skupioną F = (0; —0) w punkcie a_l i obciążeniem ciągłym q = (0; — q; 0) dla xe <0, /), (rys. 3.5 lb). Współrzędną momentu względem osi z oblicza się ze wzoru

= (x-0)R_oH(x-0)-(x-^aI)FH(x-a,) + tx-l)R_AH(x-l)-MH(x-a₂)- —\

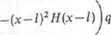
gdzie: K_a = <0: R₀- Ol reakcja w podporze 0; R_A = (0; R_A; 0) — reakcja w podporze A.

Oznaczono

(3.101)

przy czym: l — długość belki, M_g(x) — moment, p. wzór (3.99).

Maksymalne naprężenie normalne (w skrajnych włóknach) powinno spełniać warunek wytrzymałościowy

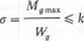
(3.102)

w którym: \V_g - wskaźnik wytrzymałości na zginanie, W_g = bh²/6 dla prostokąta, W_g = nd³fl6 dla pręta o przekroju kołowym; k_g dopuszczalne naprężenie przy zgnianiu i obciążeniu zewnętrznym niezależnym od czasu, N/m². Przybliżone równanie linii ugięcia belki (osi obojętnej) wyraża zależność

(3.103)

f(x) = —

z uwzględnieniem warunków brzegowych belki; przy czym: dla belki swobodnej podpartej y(0) = y(l) = 0; E moduł Younga; J moment bezwładności przekroju poprzecznego.

Warunek sztywności belki zginanej ma postać

(3.104)

max |y(x)l

0<x<!

gdzie,/dop — dopuszczalna strzałka ugięcia, m.

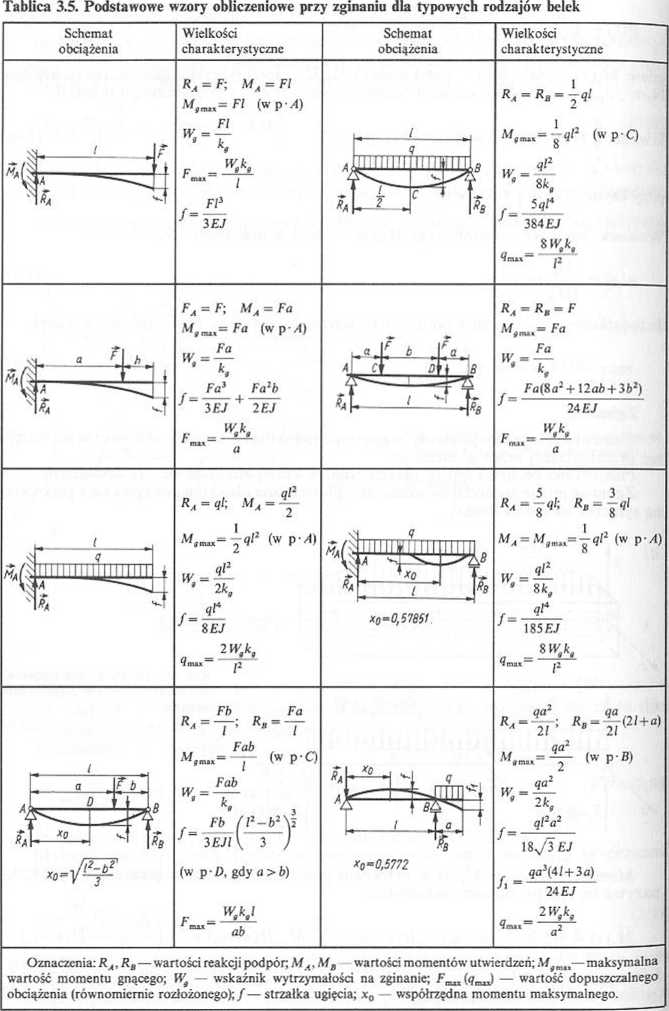
Wzory dotyczące maksymalnych wartości momentu gnącego, wskaźników wytrzymałości przekroju na zginanie, strzałek ugięcia i dopuszczalnych obciążeń dla belek podano w tabl. 3.5.

3.5.3. Wy boczenie

Pręt prosty ściskany osiowo może przy odpowiednio dużej wartości siły ulec wygięciu, mimo że wartość naprężeń jest mniejsza od granicy sprężystości. Zjawisko to jest nazywane wyboczeniem i charakteryzuje stateczność prętów prostych.

SUa krytyczna przy wyboczeniu jest to najmniejsza wartość siły ściskającej pręt osiowo, Przy której istnieje możliwość wyboczenia.

Wartość siły krytycznej Fa, przy której pręt osiowo ściskany ulega wyboczeniu °raz naprężenia krytyczne

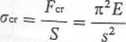
(3.106)