1tom050

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 102

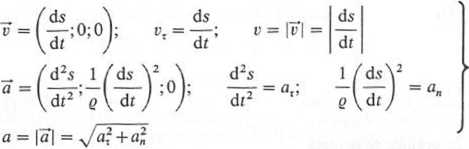
Sposób równań skończonych charakteryzuje się znajomością współrzędnych punktu M (rys. 3.21) w stałym układzie Oxyz, tj. x = x(t), y = y(f), z — z(f), a więc

(3.22)

o = j _N/x² + j;² + ż² dt

F = (x;y;ż) v = ,/x²+j>² + ż² F = (x;j;;z) u = yFTp+F _

Szczególne przypadki ruchu

Ruch jednostajny: a. = 0 s = s₀ + v,t

Ruch jednostajny zmienny: a, = const

1 ,

v, = v_0t+a,t s = s₀ + v₀,t + ja,t

(3.23)

(3.24)

(3.25)

Jeżeli: a, < 0 — ruch jednostajnie opóźniony,

a_t > 0 — ruch jednostajnie przyspieszony.

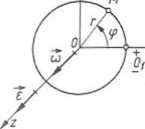
Ruch punktu po okręgu. Punkt M porusza się po okręgu o promieniu r w płaszczyźnie Oxy układu Oxyz (rys. 3.23). Współrzędna łukowa s = rip, (ip — w rad, r — w m). Stąd i ze wzorów (3.22) można otrzymać

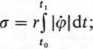
v = (r<p;0;0);

a = (rip;r(<p)²; 0)

►    (3.26)

v, = rę;    v = r\ij>\; a. = rip; a_n = r((p)²; a = rj tp^A + if>² ,

Prędkość i przyspieszenie kątowe są wektorami swobodnymi i są określone dla ruchu punktu po okręgu (rys. 3.23) następująco:

ćo = (0;0;ę>)    7 = (0;0;qż)

przy czym: S — prędkość kątowa, rad/s; F — przyspieszenie kątowe, rad/s².

Wykorzystując powyższe pojęcia, prędkość i przyspieszenie punktu M w ruchu po okręgu o środku w punkcie O (rys. 3.22) można wyrazić następująco:

tf = S x O A?;    a,=Tx O A?; ~a_n — S x (5 x 0A?)    (3.27)

dtp

Ruch jednostajny po okręgu: co. =    = const

<P = <Po+o)_zt    (3.28)

Ruch jednostajnie zmienny po okręgu d²<p

g. = —— = const dt²

1 ₂

ip = q>o+co₀.t+—&_st

co. = co₀.+£.t;

(3.29)

M

X

Rys. 3.23. Ruch punktu po okręgu koła ^ - prędkość kątowa, e — przyspieszenie kątowe

z

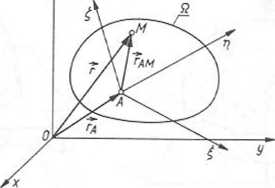
Rys. 3.24. Ruch złożony punktu

Oxyz — bezwzględny układ odniesienia,    względny

układ odniesienia, sztywno związany z ciałem S2

Ruch złożony punktu. Oznaczenia: Oxyz — układ nieruchomy; — układ ruchomy sztywno związany z ciałem Q; M — punkt ruchomy, poruszający się po ciele Q, M_n — punkt ciała £2, na którym w danej chwili znajduje się punkt M (rys. 3.24). Ruch bezwzględny — ruch M względem Oxyz; ruch względny — ruch M względem /łó/£; ruch unoszenia — ruch M_S1 względem Oxyz. Prędkość bezwzględna ~v_b jest sumą prędkości względnej ~v_w i prędkości unoszenia v_u, a więc

~v_b = v„+~v_u    (3.30)

Przyspieszenie bezwzględne a_b jest sumą_przyspieszenia względnego <?„, przyspieszenia unoszenia a_u i przyspieszenia Coriolisa a_c = 2tóxv_w, gdzie to jest prędkością kątową odcinka OM_Q lub ciała Q względem Oxyz. Zatem

a_b = a_w+’a_u+a_c    (3.31)

3.3.2. Kinematyka ciała sztywnego

Ruch postępowy. Ciało Q jest w ruchu postępowym, jeżeli prosta łącząca dwa dowolnie różne punkty ciała jest w czasie ruchu równoległa do swojego położenia pierwotnego (rys. 3.25). Właściwości:

1.    Tory wszystkich punktów są takie same, różnią się tylko o stałą.

2.    Prędkości wszystkich punktów w danej chwili są równe.

3.    Przyspieszenia wszystkich punktów w danej chwili są równe.

g

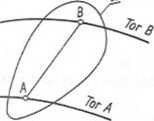
Rys. 3.25. Ruch postępowy ciała

Równanie kinematyczne ciała w ruchu postępowym, to równanie dowolnego punktu

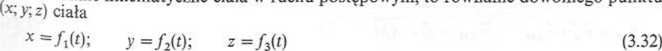
Ruch obrotowy. Ciało £2 jest w ruchu obrotowym, jeżeli istnieją co najmniej dwa różne punkty ciała, których prędkość jest równa zeru. Prostą przechodzącą przez te punkty używa się stałą osią obrotu (na rys. 3.26 oś Oz).