1tom058

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 118

Skręcanie prętów okrągłych

Pręt jest skręcany, jeżeli są przyłożone do niego pary sił działające w płaszczyznach prostopadłych do jego osi. Momentem skręcającym M_s w przekroju poprzecznym pręta w punkcie x (rys. 3.50a) nazywa się wektor

K(x) M

t M_ixH(x-a_t); 0; 0

(3.92)

przy czym: H — funkcja Heaviside’a, tj. H(x—a_i) = 1 dla x > a_t oraz II(x—aj = 0 dla x < a₍; M,- = (M_ix\0; 0) — moment skręcającej pary sił przyłożonej w punkcie a_t elementu.

Przy stałej prędkości kątowej pręta zakłada się, że £ M {aj = 0 na całej długości pręta.

i= i

Rys. 3.50. Skręcanie: a) obciążenie parami sił elementu; b) przykład wałka o przekroju kołowym; c) wykres współrzędnej momentu skręcającego

Na rysunku 3.50c jest pokazany rozkład współrzędnej M_sx(x) = [H(x—a₂)~ —H(x—a_l)']M_s momentów skręcających M_s(a_x) i M_s(a₂) przyłożonych do pręta (rys. 3.50b), przy czym M_s = |M_s(a₂)| = |jVf(a,)|.

Wprowadza się oznaczenie

M.

*= max |M_s(x)| ;

= max

0 « X < i

X M_izH(x-ad

(3.93)

w' którym: l — długość pręta, M_s{x) — moment wg wzoru (3.92).

Maksymalne naprężenia styczne w przekroju pręta (rury) nie mogą przekraczać naprężeń dopuszczalnych

₌ "i-s < _fe    (3.94)

W₀

gdzie: W₀ — wskaźnik wytrzymałości na skręcanie, m³, przy czym W₍₎ = jid³/32 dla pręta o średnicy d; W_ę = n(D*—d^A)/\6D dla rury o średnicy zewnętrznej D i wewnętrznej d.

Kąt skręcania ip części pręta zawartego między przekrojami poprzecznymi w punktach x, i x wyraża się wzorem (rys. 3.50a)

1 M_b , *_r ZM_ixH(x-a,) _j

(3.95)

<p(x) = trr<ix = J-77-dx

^v ; Gd₀ V GJg

ad/ie: M_s(x) = (M„; 0; 0) — patrz wzór (3.92); G — moduł przekształcenia postaciowego, N/m^; Jo — biegunowy moment bezwładności przekroju poprzecznego pręta, m⁴

Uwaga: J/(x)H(x₁)dx = (F(x)-F(x_l))H(x_i)    (3.96)

X,

j:

przy czym F(x) = J f(x)dx.

Wniosek: jeżeli GJ₀ = const oraz M_sx{x) = const w przedziale <x,, x>, to

(3.97)

M_s ,

<p(.x) = — (x-x.)

(jJq

Jednostkowy kąt skręcania pręta (rury), wyrażony w rad/m, musi spełniać warunek

(3.98)

1    71

max l<P(-^x)l ^ ‘Piiop ⁼ T'777T o osi    i oo

Zginanie

Element jest zginany, jeżeli siły zewnętrzne redukują się do pary sił leżącej w płaszczyźnie przechodzącej przez oś elementu.

Płaszczyzna obciążeń jest to płaszczyzna, w której znajdują się siły zewnętrzne. Zginanie proste zachodzi wówczas, gdy płaszczyzna obciążeń pokrywa się z płaszczyzną symetrii elementu (belki).

b) y
	am
	^o-(0;Ro;0)		Rfr(0;RA

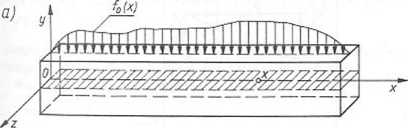
Rys. 3.51. Proste zginanie elementu: a) rozkład obciążeń; b) przykład belki zginanej

Momentem gnącym M„(x) w przekroju poprzecznym belki w punkcie x (rys. 3.51a) nazywa się wektor opisany zależnością

j= 1

M_g(x) 1 jo_; 0; £ (x-a_i)F_i>.H(x-a_i)- £ M_JZH(x-bj)+ £    ~^C,)2 ff(x-ej-

(3.99)

■H(x —c_s+1) )q