1tom056

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 114

Równanie to wyraża zasadę d’AIemberta.

Jeżeli Ss_; jest przesunięciem wirtualnym, to

(F_i+B_i+R_i)Sr_i = 0

(3.75)

Ponieważ SR.ósj- = 0, gdyż więzy są idealne, to Z(F_i+B_i)57_i = 0

Uwagi do równania (3.75):

1.    Jeżeli przesunięcie wirtualne 8s,.jest odcinkiem skierowanym, tj. 8s,. = (8x_t; 5y,; 5z,), to fi = (f.xi ^Fiy- ^Fiz) i B= -m.fe >>,; żj.

= (8co,.; 0; 0), to F,.-*M_i = (M_ix\ M_iy; M_iz) oraz_fi, r.,(/,_v; 0; 0), przy czym l_ix — moment bezwładności ciała względem osi Ox, (F_t -> M_; — oznacza, że w miejsce

2.    Jeżeli przesunięcie_wirtualne &s_t jest kątem skierowanym, czyli np. 6.s_; = ó<p_i =

F, należy wstawić AJ, itd.).

Jeżeli przyjmie się, że na układ punktów materialnych działają tylko siły mające potencjał, to energia kinetyczna E = E(q_ly...,q_s, q_It...,q_s, a potencjalna E_v = = E_v(q_v...,q^, gdzie q— współrzędne uogólnione.

Przy tych założeniach równanie Lagrange’a drugiego rodzaju ma postać

(i = l,..., s)

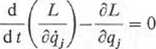
(3.76)

gdzie L = E — E_y — potencjał kinetyczny układu.

3.5. Wytrzymałość materiałów

3.5.1. Wiadomości wstępne

Wytrzymałość materiałów jest dziedziną zajmującą się ustalaniem zależności między właściwościami mechanicznymi elementów maszyn i urządzeń a siłami zewnętrznymi działającymi na te elementy. W tej części rozdziału pod pojęciem naprężenie rozumie się wartość naprężenia. Obliczenia wytrzymałościowe mają zapewnić bezpieczną oraz niezawodną pracę maszyn i urządzeń.

W przypadku każdego elementu powinny one obejmować: obliczenia ze względu na naprężenia dopuszczalne, obliczenia ze względu na odkształcenia dopuszczalne, obliczenia zapewniające stateczność, obliczenia na pełzanie. Powyższe kryteria wytrzymałościowe muszą być za każdym razem spełnione równocześnie. Nie oznacza to, że należy je wszystkie sprawdzać w konkretnych przypadkach, ponieważ sprawdzenie części warunków zapewnia spełnienie pozostałych.

Naprężenia normalne a„ są to naprężenia maksymalne obliczone z odpowiednich wzorów lub wyznaczone doświadczalnie dla obciążeń nominalnych bez uwzględnienia lokalnych spiętrzeń naprężeń, przy czym muszą one być mniejsze od naprężeń dopuszczalnych k, a zatem

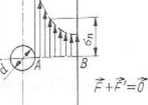
W przypadku płaskownika (rys^3.45) o szerokości h i grubości b, z otworem o średnicy d w środku, rozciąganego siłą F naprężenie

n

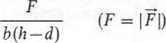
(3.77)

Rys. 3.45. Rozkład naprężeń w płaskowniku z otworem

h

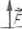
Naprężenia dopuszczalne są to naprężenia proporcjonalne do granicy plastyczności wyraźnej Q_r lub umownej Q_oz albo wytrzymałości R, na rozciąganie. Współczynnikiem proporcjonalności jest odwrotność współczynnika bezpieczeństwa x_u, w odniesieniu do granicy plastyczności lub odwrotność współczynnika bezpieczeństwa x_r„. skojarzonego z wytrzymałością na rozciąganie. Wobec tego

(3.78)

przy czym: 0_r i R_r są wyrażone w N/m².

Wartości naprężeń dopuszczalnych k zależą również od rodzaju obciążeń. W celu ich rozróżnienia dodano indeksy i oznaczono w sposób następujący: k_r — przy zginaniu, k_g — przy rozciąganiu, k, — przy ścinaniu, k_s — p;zy skręcaniu, k_d — na docisk powierzchniowy, k_c — przy ściskaniu.

W przypadku materiałów plastycznych i obciążeń stałych

k_g = k_r, k_s = k, = 0,6 k,

Współczynnik x„ = x_lx₂x₃x_i, w którym: x, — współczynnik pewności założeń, x₂ — współczynnik ważności elementu, x₃ — współczynnik jednorodności materiału, -*4 — współczynnik zachowywania wymiarów.

Obliczenia wytrzymałościowe na dopuszczalne odkształcenia

W wielu przypadkach warunkiem prawidłowego działania maszyny lub urządzenia jest zachowanie dostatecznej sztywności, czyli niedopuszczenie do nadmiernych odkształceń. Typowymi przykładami są wały pędne, w których kąt skręcania wału o długości

1 m nie może przekraczać — stopnia, a zatem gdzie: G — moduł Kirchhofla, N/m²; J₀ — biegunowy moment bezwładności przekroju poprzecznego wałka, m⁴; M_s — moment, N-m.

Naprężenia przy skręcaniu wylicza się ze wzoru

8»