1tom047

3. MECHANIKA TECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁÓW 96

3.2.8. Środek sil równoległych

Niech na ciało sztywne działa układ sił równoległych    i niech A_J będzie punktem

zaczepienia siły Fj, (j = IZakłada się, że siły nie będą przesuwane wzdłuż ich prostych działania.

Środkiem dwóch sil równoległych jest nazywany punkt przecięcia się prostej działania wypadkowej tych sił z prostą łączącą początki sił.

Z tej definicji oraz konstrukcji wyznaczania prostej działania dwóch sił równoległych wynika algorytm wyznaczania środka układu sił równoległych.

__ Środek S₁ sił F_l i F₂ jest punktem przecięcia się prostej działania wypadkowej F_n = F, + F, z prostą przechodzącą przez punkty A, i A₂ (rys. 3.11 a). Środek S₂ sił F_rl

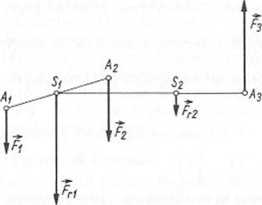
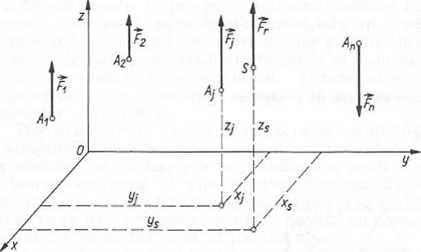
Rys. 3.11. Wyznaczanie środka sil równoległych: a) graficzne; b) ilustracja geometryczna do analitycznego obliczania współrzędnych środka

i Fj jest punktem przecięcia się prostej działania wypadkowej F_r2 = F_rl + F, i prostej przechodzącej przez punkty i A₃. Postępując tak dalej, wyznacza się środek S„_, (krótko Sj sił F,„_₂ i F„, który jest punktem przecięcia się wypadkowej F, = F,„_₂ + F„ z prostą przechodzącą przez punkty S„_, i A„.

W celu wyznaczenia współrzędnych środka sił równoległych przyjęto układ Oxyz tak, żeby oś Oz była równoległa do prostych działania sił (rys. 3.1 lb). W tym układzie współrzędnych F_; = (0;0; kjJ, (j = 1Zatem F_g = (0;Ó;£F_J=).

Punkt zaczepienia siły Fj oznaczono Aj(Xj; yy, z^. Współrzędne środka sił równoległych wyznacza się ze wzorów

£F,, ’

y* =

ZFj-J;

ZFjSj

Z.F,,

(3.6)

Powyższe wzory mają sens, gdy ZF_JS # 0.

3.2.9. Tarcie

Tarciem zewnętrznym nazywa się całokształt zjawisk występujących między stykającymi się powierzchniami ciał stałych, spowodowany działaniem siły dociskającej te ciała oraz siły przemieszczającej je względem siebie (tarcic kinetyczne), bądź też usiłujących je przemieścić (tarcie statyczne) (rys. 3.12).

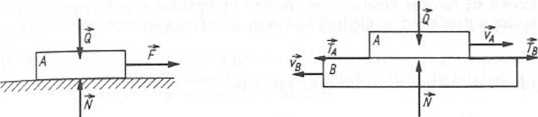
Rys. 3.12. Ciało sztywne A z więzami tarciowymi (płaszczyzna chropowata)

Rys. 3.13. Zwroty sił tarcia przyłożonych do ciał w^r zależności od ich prędkości

Siła F przesuwa lub zamierza przesunąć ciało względem podłoża, siła N jest reakcją podłoża, zaś Q — siłą dociskającą. Opór przy przemieszczaniu lub zamiarze przemieszczania się ciał względem siebie jest siłą, ponieważ do scharakteryzowania go należy podać trzy cechy, takie jak dla wektora. Siłę tę nazywa się silą tarcia T.

Zwrot siły tarciajest przeciwny do ruchu (prędkości) ciała lub ruchu zamierzonego (rys. 313)._Siła tarcia T_A jest przyłożona do ciała A, zaś siła T_B do ciała B, przy czym T_a + T_b = 0, Q + N == 0,    > 0, v_B > 0.

Siła tarcia statycznego jest to siła (reakcja) przeciwstawiająca się przemieszczaniu ciał względem siebie, mimo że ciała te są w spoczynku (rys. 3.14).

Zakłada się, że proste działania sił Tj F_są równolegle, a ich odlcglośćjcstjra tyle mała (można przyjąć w przybliżeniu), że siły T i F tworzą dwójkę zerową T+F = 0, przy czym wartość siły F jest z pewnego przedziału, tj. Fe(0, F₀), gdzie F₀ jest graniczną wartością siły F, przy której ciało A pozostaje jeszcze w spoczynku.

Tarcie, przy którym siła tarcia T = — F₀ jest zwane tarciem statycznym rozwiniętym. Wartość siły tarcia jest wtedy największa i wynosi wg Coulomba

(3.7)

T= pN

gdzie fi — współczynnik tarcia.

Wartość współczynnika tarcia zależy od rodzaju ciał, nierówności powierzchni trących się, od czynnika (smaru) znajdującego się między powierzchniami oraz od wartości prędkości względnej przesuwających się ciał w przypadku tarcia kinetycznego.

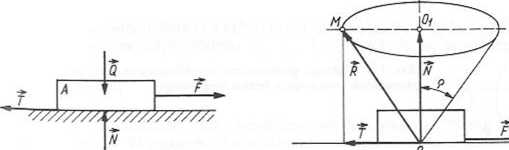
W celu zobrazowania narastania wartości siły tarcia do wartości maksymalnej w przypadku tarcia statycznego wprowadzono pojęcie stożka tarcia i oznaczono

R = T + N

gdzie: N — reakcja podłoża, T — siła tarcia rozwiniętego (N = OO_l, T = 0,3-/ na rys. 3.15).

o

Rys. 3.14. Siła tarcia T— reakcja więzów tarciowych

Rys. 3.15. Stożek tarcia

Reakcja R„ wewnątrz stożka — tarcie statyczne nierozwinięte; reakcja R na pobocznicy stożka tarcie statyczne rozwinięte

7 Poradnik inżyniera elektryka tom 1