272 273

272 Podejmowanie decyzji w warunkach niepełnej informacji

Próbą połączenia tych dwóch skrajności jest reguła Hurwicza, w której wykorzystuje się współczynnik ostrożności. Współczynnik ten oznaczony symbolem y jest liczbą z przedziału 10, 1J opisującą niechęć decydenta do podjęcia ryzyka. Wartość 1 charakteryzuje skrajną awersję do ryzyka, wartość 0 — skrajną skłonność do ryzyka.

Oznaczymy minimalną wypłatę dla decyzji i symbolem a,, natomiast wypłatę maksymalną — symbolem A,-. Zauważmy, że wartości minimalne były wykorzystane w regule max—min, wartości maksymalne — w regule max-max. Dla kolejnych decyzji obliczamy wartość:

H,{y) = a_ry+Ai(l-y).

Reguła Hurwicza

Wykorzystując kolejne wiersze macierzy wypłat, znajdujemy dla każdej decyzji o numerze i wartości: a,, A, oraz hl,(y). Wybieramy tą decyzją, dla której wartość II,(y) jest najwiąksza. W przypadku niejednoznaczności rekomendujemy wszystkie decyzje, dla których spełniony jest powyższy warunek.

Zastosujemy regułę Hurwicza, wykorzystując dane liczbowe z przykładu 5.3. Przypuśćmy, że decydent chce dokonać wyboru decyzji dla y = 0,5. Wykorzystujemy obliczone w podrozdziale 5.3.1 wartości a, oraz A, do wyznaczenia wartości H,(0,5). Przebieg obliczeń przedstawiamy w tablicy 5.8.

Decyzją rekomendowaną przez regułę Hurwicza jest uprawa 3.

Łatwo zauważyć, że dla wartości skrajnych współczynnika ostrożności otrzymujemy omawiane uprzednio reguły decyzyjne: dla wartości współczynnika y = 0 reguła Hurwicza sprowadza się do reguły max-max, a dla y=l — do reguły max-min. Tak więc te dwie wcześniej omawiane reguły są szczególnymi przypadkami ogólniejszej reguły Hurwicza.

Prześledzimy obecnie, w jaki sposób zmiany wartości współczynnika ostrożności wpływają na zmianę decyzji rekomendowanych na podstawie reguły Hurwicza. Rozpatrzmy funkcję:

//,(y) = 8y+12(1 -y).

Tablica S.8

Rodzaj uprawy	Warunki pogodowe			min	max	Hjy)
	susze	normalne	deszcze
i	8	10	12	8	12	10
2	10	11	7	7	11	9
3	9	13	8	8	13	(ńk5)<— max
4	11	10	6	6	11	8,5
5	10	10	9	9	10	9,5

Jest to funkcja liniowa zmiennej y. Dla y = 0 mamy /-/, (0) = 12, dla y- 1 jest //,(y) = 8. Wykres funkcji w interesującym nas przedziale [0, 1] otrzymujemy, łącząc odcinkiem znalezione punkty o współrzędnych (0, 12) i (1, 8). Wykres funkcji H,(y) przedstawiono na rys. 5.3.

Rysunek 5.3

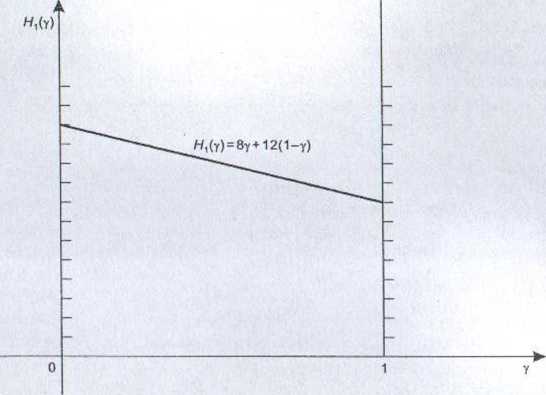
W podobny sposób otrzymujemy wykresy pozostałych funkcji //₂(y), ..., H_s(y). Wykresy wszystkich funkcji H,(y) przedstawiono na rys. 5.4.

Zgodnie z regułą Hurwicza przy ustalonej wartości y wybieramy tę decyzję i, dla której wartość funkcji //,(y) jest największa. Możemy więc zdefiniować nową funkcję H jako maksymalną wartość wszystkich funkcji H,. Funkcję H, przedstawioną na rys. 5.5, określamy następująco:

W(y) = max {H,(y), H₂(y), H<(y), W₄(y), //₅(y)}.

Interesują nas punkty 4, fi i C. Punkt 4 należy do wykresu funkcji //₃(y), punkt C należy do wykresu W₅(y). Punkt fi to przecięcie wykresu funkcji i W_s, więc do wyznaczenia jego współrzędnych trzeba rozwiązać proste równanie liniowe:

8y+ 13(1 -y) = 9y+ 10(1 — y).

Jego rozwiązaniem jest y = V.,.

Odcinek 4fi wykresu funkcji H to fragment wykresu funkcji H>„ odcinek fiC to fragment wykresu funkcji II_s.