280 281

280 Podejmowanie decyzji w warunkach niepełnej informacji

macierzy wypłat równocześnie i zachowują się racjonalnie, usuwając ze zbioru strategii własnych oraz konkurenta strategie zdominowane. Zaczynamy od rozpatrzenia strategii, jakimi dysponuje Gracz I.

Porównujemy najpierw strategię 5^|’ ze strategią Ó⁽²⁾. Jeżeli Gracz II wybierze strategię to wypłata dla Gracza I będzie w obu przypadkach taka sama, równa 1. Tak więc przeprowadzone porównanie wskazuje, że o ile Gracz 11 wybierze strategię S*,',', obie porównywane strategie są dla Gracza I równie dobre. Jeżeli Gracz II wybierze strategię S¹²,*, to przy zastosowaniu przez Gracza I strategii otrzyma on wypłatę 2, a przy zastosowaniu strategii S*²⁾ — wypłatę 0. Tak więc o ile tylko Gracz II wybierze strategię S**, Graczowi I korzystniej jest wybrać strategię S^<\^>. Jeżeli natomiast Gracz II wybierze strategię St-fj, to przy zastosowaniu przez Gracza I strategii S*!’ otrzyma on wypłatę 4, a przy zastosowaniu strategii S<²⁾ — wypłatę 5. Tak więc o ile tylko Gracz II wybierze strategię S¹,³,¹, Graczowi I lepiej wykorzystać wówczas strategię S*)’.

Z tego szczegółowego porównania wynika, że nie ma jednoznacznej odpowiedzi na pytanie, czy strategia 5*|’ Gracza I jest lepsza od strategii ó^<2), stąd możemy stwierdzić, że dla Gracza 1 ani strategia S*]¹ nie jest zdominowana przez strategię S*²’, ani strategia S*,’ nie jest zdominowana przez strategię S*}¹. Są to więc strategie niezdominowane.

Z kolei dla Gracza I porównujemy strategię S^<|⁾ ze strategią Stosując strategię 5‘J*, w zależności od strategii zastosowanej przez Gracza 11, Gracz 1 otrzymuje wypłaty w wysokości 1, 2 lub 4. Odpowiednie wypłaty dla Gracza 1 przy zastosowaniu strategii S*³* wynoszą, odpowiednio, 0, 1 i -1. Widać stąd, że niezależnie od wyboru strategii przez Gracza II, Graczowi 1 korzystniej jest wybrać

strategię S*}’,

która dominuje nad Strategię S*}¹ jako strategię zdominowaną

usuwamy ze zbioru strategii Gracza 1. Macierz wypłat po usunięciu strategii zdominowanej S'f ma postać:

W =

2 4 0 5

Ponieważ wyczerpaliśmy chwilowo możliwości porównywania strategii dla Gracza I, więc przechodzimy do porównywania strategii dla Gracza II. Biorąc pod uwagę strategie S*,¹,’ i S^f,²1⁾, nie stwierdzamy między nimi dominacji — są to więc strategie niezdominowane. Porównując natomiast i S*,³’, stwierdzamy, że S¹,¹,’ dominuje nad S*,³’ (pamiętamy przy tym, że analizując macierz wypłat dla Gracza II, interpretujemy ją jako macierz strat). Wynika stąd, że strategię S*³* należy usunąć ze zbioru strategii Gracza II. Po tej redukcji macierz wypłat ma postać:

I 2

W =

1 0

Wracamy do analizy macierzy wypłat z punktu widzenia Gracza 1. Pierwszy wiersz macierzy W odpowiada strategii S^, drugi — strategii 5'j²/. Widzimy teraz, że niezależnie od wyboru strategii przez Gracza II, dla Gracza I korzystniej jest posługiwać się strategią S*)’. Strategia 5']' dominuje więc teraz nad strategią 5® i dlatego S’*,' usuwamy ze zbioru strategii Gracza I. Zwróćmy przy tym uwagę, że porównanie strategii S¹]' ze strategią S^^ł przyniosło poprzednio inny wynik ze względu na to. że przy pierwszym porównaniu trzeba było uwzględnić również możliwość wyboru przez Gracza II strategii S¹^, która następnie okazała się dla lego gracza strategią zdominowaną. Po wykreśleniu strategii dla Gracza I macierz W ma następującą postać:

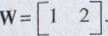
Obecnie zajmiemy się analizą zredukowanej macierzy wypłat z punktu widzenia Gracza 11. Ma on dwie możliwe strategie, obie przynoszące straty. Gorsza jest strategia stąd usuwamy ją ze zbioru strategii Gracza II. Tak więc końcowa macierz wypłat ma postać:

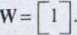
Przez analizę i redukcję macierzy wypłat otrzymujemy rozwiązanie gry najkorzystniejsze dla obu jej uczestników. Kandydat 1 i Kandydat II powinni wybrać, odpowiednio, strategie 5‘J’ i Wtedy spodziewany przyrost głosów dla Kandydata I wyniesie 1%, co spowoduje spadek liczby wyborców głosujących na Kandydata II również o 1%. Wybór innej strategii dla Kandydata I, przy założeniu racjonalnego zachowania się Kandydata II, jest mniej korzystny. Podobnie strata, poniesiona przez Kandydata II przy wyborze przez niego innej strategii niż 5'J’, przy założeniu racjonalnego zachowania się Kandydata I, będzie większa. Przedstawione powyżej uzasadnienie wskazuje na to, że są to strategie optymalne zarówno dla Kandydata l, jak i dla Kandydata II.

Wypłata, jaką otrzymają gracze po wybraniu strategii optymalnych, nazywana jest wartością gry. Jeżeli wartość gry jest równa 0, to taką grę nazywamy grą sprawiedliwą. Rozpatrywana powyżej gra nie ma tej własności.

5.4.2. Punkt siodłowy

Poszukiwanie strategii zdominowanych często doprowadza do redukcji macierzy wypłat, lecz zazwyczaj pozostają jeszcze pewne strategie niezdominowane, zarówno dla Gracza I, jak i dla Gracza II. W takiej sytuacji w celu rozwiązania gry wykorzystamy regułę max-min dla Gracza I oraz regułę min-max dla Gracza II. Posługiwanie się przez Gracza I regułą max-min uzasadnione jest jego obawą przed niekorzystnymi możliwymi decyzjami Gracza II. Zastosowanie reguły