274 275

v!^

274 Podejmowanie decyzji w warunkach niepełnej informacji

g#:

Rysunek 5.4

Rysunek 5.5

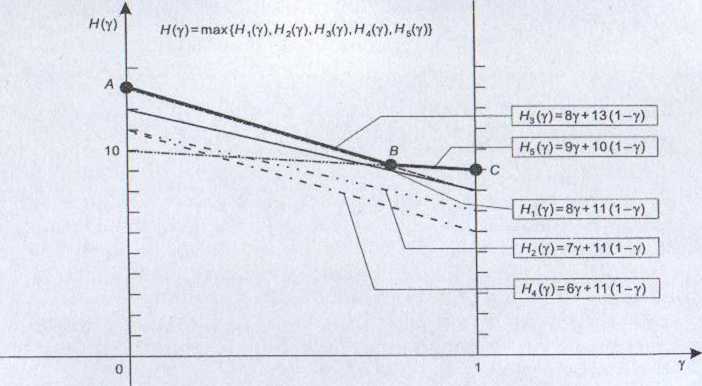
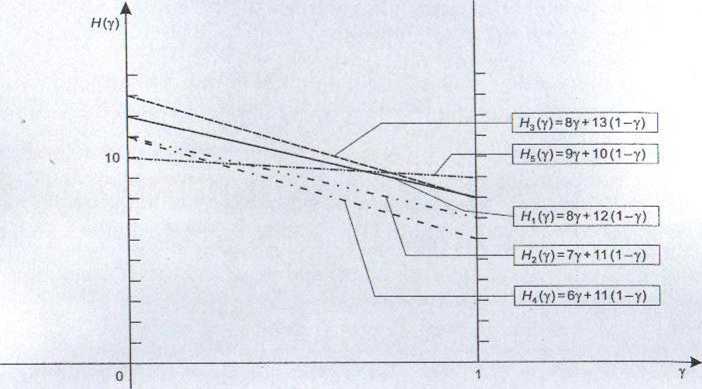
Dla wartości współczynnika ostrożności z przedziału [0, V₄) optymalną decyzją zgodnie z regułą Hurwicza jest uprawa 3. Dla y = ³/,₄ mamy dwie decyzje optymalne: 3 oraz 5. Dla wartości y z przedziału (V₄, 1| optymalną decyzją jest uprawa 5.    f§

5.3.3. Reguła braku dostatecznej racji

Jeżeli nie znamy prawdopodobieństw zaistnienia poszczególnych stanów natury, to możemy przyjąć, żc są one równie prawdopodobne i zastosować regułę braku dostatecznej racji (Laplace’a).

Reguła Laplace’a

Wykorzystując kolejne wiersze macierzy wypłat, znajdujemy dla każdej decyzji oczekiwaną korzyść, przyjmując, że realizacje kolejnych stanów natury są równie prawdopodobne. Wybieramy tą decyzją, dla k tórej oczekiwana korzyść jest największa. W przypadku niejednoznaczności rekomendujemy wszystkie decyzje, dla których spełniony jest powyższy warunek.

Zastosujemy regułę Laplace’a do danych z przykładu 5.3. Wyniki obliczeń przedstawiono w tablicy 5.9. Obliczamy wartości oczekiwane dla kolejnych decyzji.

Spośród znalezionych w ten sposób liczb wybieramy największą (tablica 5.9).

Tablica 5.9

Rodzaj uprawy	Warunki pogodowe			Oczekiwana korzyść
	susze	normalne	deszcze
i	8	10	12	(30/5)<— max
2	10	11	7	28/3
3	9	13	8	(30/3)<r- max
4	11	10	6	27/3
5	10	10	9	29/3

Decyzjami rekomendowanymi na podstawie reguły Laplace’a są uprawy 1 i 3.

5.3.4. Reguła minimalnego żalu

Punktem wyjścia reguły decyzyjnej minimalnego żalu (Savage’a) jest chęć zminimalizowania utraconych korzyści, związanych z podjęciem decyzji, która okazała się nietrafna w kontekście zrealizowanego stanu natury. Chcąc wykorzystać tę regułę, przeprowadzamy obliczenia wstępne. Będą nas interesować maksymalne wartości w kolumnach macierzy wypłat, które oznaczymy jako w) dla j= 1, ..., n. Otrzymujemy w ten sposób maksymalne korzyści, jakie decydent może uzyskać, jeżeli zrealizują się kolejne stany natury, a decydent uprzednio trafnie je przewidzi.