Matematyka 2 99

398 V. Elementy rachunku prawdopodobieństwa

c)    EX= 1, KY-5,5, VarX = 59. VarY^24.75 .

d)    zależne;

O	*■ 1	-10	0	10
	P(X= x,|Y -0) |	2/9	V9	4/9

*	(-ao. I0>	<-io.o>	(0.l0>	(10,*)
Fx(x|Y = 0)	0		V9	1

F(xrY = 0) = 20/9. Var( X|Y- 0)- 5000/81 *61.7: 0 cov(X,Y) - -5,5, p_{v v} * -0,14;

B)	v | 0	10	x I -10	0	10
	E(Xly) || 20/9	0	n(Ylxl| 20/9	25/4	30/7

h>y-5,5--^(*-l). y-5.5 = ^(* 5.5)

2.

a) _P, = 1/16. p_:-15/16. p, -9/16. p₄ = 1/16. p, = 7/16. p, = 0;

b) f_x(x)»

4x^J O < x < I

My)

„ J 4y< I - y² 1 0

- jr I tlili 0< y < I

dla y<0 v yłl;

0 dla x<0 v x>l c) KX -4/5. HY =H/\5, VarX = 2/75. VarY= I1/225; d| /ale/nc;

e)Dla ye(U.I)    f_x(x|y) = J^2x/<^|->‘>    >’^<x<ł

0 dla x<y v

Dlaxc|0.l) f_vly|x)=

x>l.

*■ dla 0<y<x dla y<0 v y>x

h(X|y)- ²⁽X‘ ^±^l-^>-> dla y6(0.1); NY;x) = 4* dla 0<x<l: •My * w    •'

f) cov( X.Y)-4/225. p_x>v= 4/^66 *0,49; g) jak w punkcie cl;

y-JLJil*

•    15

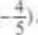
3. fix,y)=xc *⁰"¹ . x>0, y>0. 4 a) niezależne (1 mcskorcłowanc), b)niezależne, cl zależne i mcskorcłowanc. d) zależne 1 mcskorcłowanc.

5.    cov(X.Y»<10;    7.34:    8 29;    9. a) -12. b) I. •!.•!; c) •!:

11 a)(EX.EY). b)lp = l. cl (p|=0. d)y = 2x-3.

VI. ELEMENTY STATYSTYKI MATEMATYCZNEJ

1. TRZY ROZKŁADY WAŻNE W STATYSTYCE.

Wariancja średniej arytmetycznej, wiedzą o

wariancji uzupełnimy teraz o wariancją sumy n zmiennych losowych (ZL)i ich średniej arytmetycznej (stosujemy skróty z rozdziału V).

TWIERDZENlh I I. Jeżeli ZL X_)fX_:^..,X_n są niezależne i mają jednakowe wartości oczekiwane i jednakowe wariancje:

nx, - F_X₂ - ..= EX_n =m. VarX₍ =VarX₂ =...= VarX_n =o^:

(w szczególności ma to miejsce, gdy ZL X, mają ten sarn rozkład pr-slwa), to:

1)    wartość oczekiwana i wariancja ich sumy

s„=x,₊x_!+-₊x„-£x,

icst n-krotnością odpowiednio wartości oczekiwanej i wariancji składników X,:

(1.1)    HS„ =nEX₍ = np, VarS_n = n* VurX, = no^:,

2)    ich średnia arytmetyczna

— ^der 1    I sr* I

x_n=I(X,+x₂₊-₊x_B).i2;x₁-^s_n