Zarz Ryz Finans R1387

1 3. Taksonomia modeli wyceny opcji 387

Dalsze wnioski z modelu Blacka-Scholesa wyciągniemy, zagłębiając się nieco bardziej w problem wyceny obojętnej na ryzyko.

1 3. Taksonomia modeli wyceny opcji 387

*

Cena

opcji    Cena opcji kupna

C    wg B lacka

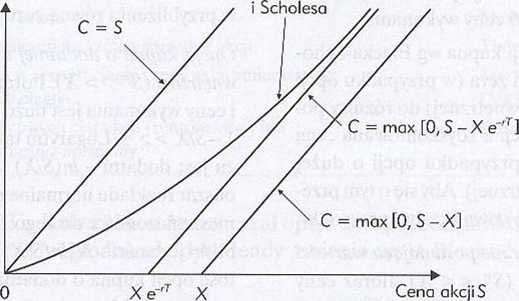
Ceny opcji kupna wg Blacka i Scholesa leżą poniżej wartości maksymalnej C = S (z wyjątkiem S = 0), a powyżej wartości minimalnej C = max[0, S -Xe~^rT], Zauważmy, że krzywa ceny opcji kupna wg Blacka i Scholesa w funkcji ceny akcji zbiega się asymptotycznie z prostą C = max[0, S - Xe ^,r].

Ilustracja 13.4. Cena opcji kupna wg Blacka i Scholesa dla różnych cen akcji

- przy ustalonych parametrach stopy procentowej, współczynnika zmienności i czasu do wygaśnięcia

Na marginesie

Interpretacja wzoru Blacka-Scholesa

Równanie 13.12 możemy przeformulować w taki sposób, by przedstawiało wartość opcji kupna poprzez warunkową wartość oczekiwaną¹:

C = e“E(S* > X), (S* > X)-e-% (S* > X)

Pierwszy człon równania jest iloczynem dwóch czynników:

•    zdyskontowanej oczekiwanej wartości akcji w dniu wygaśnięcia opcji pod warunkiem, że cena akcji w tym terminie przekracza cenę wykonania;

•    prawdopodobieństwa, że w dniu wygaśnięcia opcji cena akcji będzie wyższa od ceny wykonania.

1

Dopóty, dopóki uczestnicy rynku są obojętni na ryzyko.