Zarz Ryz Finans R1389

1 3. Taksonomia modeli wyceny opcji 389

1 3. Taksonomia modeli wyceny opcji 389

Tabela 13.2. Modele odchodzące od poszczególnych założeń Blacka i Scholesa
Założenie	Autorzy, którzy od niego odstcjpili
Brak dywidendy	Merton (1973)
Brak podatków i kosztów transakcyjnych	Ingersoll (1976)
State stopy procentowe	Merton (1973)
Nie ma ograniczeń na krótką sprzedaż akcji	Thorpe (1973)
Rynek dziaia w sposób ciągły i ceny akcji zmieniają się w sposób ciągły	Merton (1976) Cox i Ross (1976)
Rozkład końcowych cen akcji (rentowności) jest logarytmiczno-normalny	Jarrow i Rudd (1982)

W 1973 r. Robert Merton rozważa! opcje europejskie na akcje przynoszące dywidendę. Uwzględnienie dywidendy zmienia wzór Blacka-Scholcsa następująco:

- e~^rlX*N-

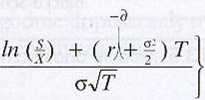
(13.14)

-3

C

+ (/-l+?)r

gdzie 5 oznacza stalą stopę dywidendy. Jak pokazuje równanie 13.14, dywidenda zmniejsza wartość, jaką akcja przedstawia dla posiadacza opcji, o wartość bieżącą przepadlych dywidend, oraz zmniejsza koszt trzymania akcji o strumień dywidend, które zostałyby otrzymane.

W 1975 r. Jonathan Ingersoll rozwinął model Mertona uwzględniający dywidendę jeszcze bardziej, rozważając świat, w którym dywidendy są opodatkowane według stopy x, a zyski kapitałowe nie są opodatkowane:

^c-H *£^tf)r

,u-t)

In (f)

oJT

(13.15)

W pracy z 1973 r., w której Merton uwzględnił wpływ dywidendy, rozważał także zmienne stopy procentowe; uogólnienie to zmienia wzór Blacka-Schole-sa do postaci:

C = S N-

-lnB(T)+ (6²!₂)T

l^fl (f) +Q»^Z] Wf :

B(7)

iS²H)T

- ihx'N-

In (!)

-łnB(T)

+

(13.16)

gdzie B(T) oznacza wartość nie narażonej na lyzyko niewypłacalności obligacji zerokuponowej z terminem płatności równym terminowi wygaśnięcia opcji,