0495

497

§ 1. Całki niewłaściwe o granicach nieskończonych

Scałkujemy te nierówności uwzględniając, że

(12)

Otrzymamy

c»+i)it

J l+.4sin²;r

lift

-J

dx

1+A sin²¹

7T

1/T+a

n¹ 7c^1łl

<»+l)«

<    / /(¹) dx <

nrr

(«+!)»

^l + nM

Sumując teraz względem n od 0 do oo, mamy

s

n^aTz^1+l

VT+(h+W^

Ponieważ obydwa skrajne szeregi są zbieżne lub rozbieżne jednocześnie z szeregiem

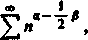
o

więc to samo możemy twierdzić o całce.

A więc całka nasza jest zbieżna dla fi >2 (a+1) i rozbieżna dla fi < 2 (<x+1). 11) To samo dla całki

/

x¹dX

1+¹^ |sin¹|

(«, fi > 0)

Metoda rozumowania jest taka sama jak w poprzednim przykładzie. Musimy tu jednak rozpatrzyć całkę [patrz 288, 14)]

/

dx

1+A sin x

2 ^lni.^+ j^A1 JL) (A > l)

^A²-\

zamiast całki (12). Ponieważ dla A -¹■ co

^(A+l/A^-i) . In A }/A²-l    ' 41

więc wystarczy porównać daną całkę z szeregami

y_;|ł ln (n-t-1/

V («+l/

s

(«+!)¹

In

czyli właściwie z szeregiem

ln n

„fi-¹

Odpowiedź. Całka jest zbieżna dla fi>¹+1, a rozbieżna dla fi < a+1. Przykłady 6), 7), 9), 10), 11) pochodzą od G. H. Hardy’ego.

1

Łatwo to wyprowadzić z 288, 10) lub 309, 9).