0477

(2)

(2)

479

§ 1. Całki niewłaściwe o granicach nieskończonych

2) Zbadajmy zagadnienie, dla jakich wartości wykładnika A>0 istnieje całka niewłaściwa

+ 30

f 4 ^(fl>0)-

n ^

Niech A^l. Wówczas

A

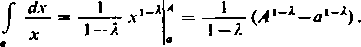
Gdy A -*■ oo, wyrażenie to ma granicę oo lub równą liczbie skończonej -5—— a¹-¹ w zależności od tego,

A— 1

czy A<1 czy też A>1. Gdy A = 1, mamy

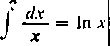
A

= In A—In a,

gdy A -¹■ 00, otrzymujemy granicę 00.

A więc dla A>1 całka (2) jest zbieżna (i jest równa

A-l

a'~^x), a dla A < 1 rozbieżna.

Podobnie do (1) definiujemy także całkę funkcji /(x) w przedziale od — 00 do a:

(3)    f/W dx - lim ff(x) dx    (A' < a),

^J    A'—00 ^

-OO    A¹

jak również całkę funkcji f(x) w przedziale (—00, +00):

400    A

i f (x) dx — lim f /(x) dx .

*'    .4'—OG J

^4—+00

Zachowujemy tu też terminologię podaną przy definiowaniu całki (1). W ostatnim przypadku biorąc dowolne a możemy przyjąć:

J f(x)dx = jf(x)dx+Jf(x)dx

a więc istnienie granicy przy A — 00 i .4 -> + oo dla całki po lewej stronie jest równoważne istnieniu poszczególnych granic (1) i (3) całek występujących po prawej stronie wzoru (¹). Można więc określić całkę w granicach od —00 do +00 za pomocą równości

+00    a    +00

J f(x)dx = jf(x)dx+ jf f(x)dx

—00    —00    a

przy założeniu, że poszczególne całki po prawej stronie istnieją. Definicja ta nie zależy w iS' tocie od wyboru punktu a.

1

Z wyjątkiem przypadku, gdy obie te całki są równe nieskończoności, lecz mają różne znaki.