0479

§ 1. Całki niewłaściwe o granicach nieskończonych

48 i

Podobnie

f cos bxdx =    .*-«

•’    a²+b¹

a²+b²

2) fTTT = \^ 1" ^X^^X^l⁺ⁱ +—arctEC^+D-ł-o ^,+* L 41/2 x²-x^Z+l 21/2

—arctg(A:j/2-1)    =—*7=-

2 j/2    Jlo 2l/2

3)    | -4r sin — d* = cos —

./ V²    V    V

= 1.

4) f sin.* dx. Funkcją pierwotną jest tu —cos x, symbol cos at|” nie ma jednak sensu, bo cos .v

O

nie dąży do żadnej granicy gdy x -► oo, a więc całka nie istnieje.

30

x ln ,v

⁵> I

(1+*²)³

dx,

Po scałkowaniu przez części i przez rozkład na ułamki proste otrzymujemy funkcję pierwotną

FW-J

x In a* (l+x²)³

dx

ln x

1

— ------r --- ln x--- ln (1 +.v²)-t- — --

4    (1+*²)²    4    8    8 l-kv²

Gdy x -*■ 0, wówczas lim F(x) ■» -g-. Tę właśnie granicę przyjmujemy jako wartość funkcji dla .v = 0. Z drugiej strony, F(+ oo) = 0. A więc wartością całki jest — ^ .

6) Obliczyć objętość i pole powierzchni bocznej bryły otrzymanej przez obrót hiperboli xy --- 1 dokoła osi. x, dla części wyznaczonej z nierówności x > 1.

Skończona część bryły odpowiadająca zmianie x od 1 do A (A>1) ma objętość i pole powierzchni bocznej równe odpowiednio

V* = «

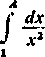
S_x = 2tt

1 +\dx.

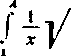
x‘

Naturalne będzie przyjęcie objętości V i pola powierzchni bocznej S całej (rozciągniętej do nieskończoności) bryły jako granicy tych wielkości, czyli

1    J

Jednakże, podczas gdy pierwsza z tych całek jest zbieżna [470, 2)] i otrzymujemy dla objętości skończoną wartość 77, druga jest rozbieżna, co wskazuje na to, że pole powierzchni bocznej jest nieskończone. Aby się o tym przekonać wystarczy zauważyć, że

A

S_A> 2tt f — = 2tt ln A

J x

i

i S_A dąży do oo, gdy A -> oo.

7) W początku współrzędnych O umieszczona jest masa m, która przyciąga punkt materialny M o masie 1, znajdujący się na osi x w odległości x od O, z siłą 31 Rachunek różniczkowy