0489

491

§ 1. Całki niewłaściwe o granicach nieskończonych

w punktach nr. (n = 1,2, 3, ...), więc naturalne będzie właśnie te liczby przyjąć jako A„ i rozpatrywać szereg

co (n4-l)n

Z /

(7)

nn

im+iyn .    ^

Dokonując w wyrazie ogólnym v_n = f ^Sl X dx podstawienia x = mc+t, otrzymujemy

mc ^x

dt.

sin / mc+t

Widać stąd, że wyrazy szeregu przyjmują na przemian znaki dodatnie i ujemne i maleją co do bezwzględnej wartości. Poza tym dla n>0

Kl = fdt< j" — <¹ = —,

J mc + t    J mc n

o    o

a więc ciąg wartości bezwzględnych wyrazów szeregu dąży do zera wraz ze wzrostem wskaźnika. Szereg (7) jest szeregiem naprzemiennym i na mocy znanego twierdzenia Leibniza [381] jest zbieżny. Oznaczmy jego sumę przez /. Dla dowolnego e>0 można więc znaleźć takie N, że dla n > N zachodzi nierówność

(8)

dx-I

< e .

Teraz zakończenie dowodu istnienia całki łatwiej jest przeprowadzić w języku e—6. Niech będzie A>Nir. Istnieje więc taka liczba naturalna n₀, że n₀n<A<(n₀+l) ic, przy czym oczywiście n₀>N. Po-

A

nieważ funkcja sin x zachowuje stały znak w przedziale od n₀ic do (n₀+1) 7c, więc całka J jest zawarta

o

*o« (Ho-t-l)ft

między całkami J i J , z których każda leży z uwagi na (8) — między I—sa I+e. To samo można

o o

A

powiedzieć o całce J . Mamy więc ostatecznie dla A >Nit

O

a więc istnieje całka niewłaściwa

(m~dx

* x o

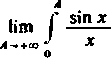
dx = /(>).

c (sin x|

Wiemy już [476], że całka ta jest warunkowo zbieżna, to znaczy że całka J -dx jest rozbież-

o ^x

na. Łatwo można się o tym przekonać przedstawiając całkę w postaci szeregu. Rzeczywiście, gdyby całka ta była zbieżna, to mielibyśmy jak poprzednio

CO (A+1)7T

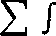
n-0 wir

M²Ldx

X

sin t mc+t

n—0 O

dt,

1

Interesuje nas tu (tak jak w poprzednim ustępie) tylko zagadnienie zbieżności tej całki. Zobaczy

2

my później, że / ¹= ir/2.