0522

524

XIII. Całki niewłaściwe

Wskazówka. We wszystkich przykładach należy skorzystać z podstawienia Abela [284].

10) Zagadnienie zbieżności całek

f-—. f -- (A>0), a>\, A> (0

^J xhrx , x ln x ln*(ln x)

^x(ln x)

rozwiążemy natychmiast, gdy za pomocą podstawienia

l = ln x, u = ln (ln x) .

sprowadzimy je do całek

( dt fdu

Ina    I«(la4)

Obydwie całki są zbieżne dla Ż>1 i rozbieżne dla A<1.

W następnych przykładach będziemy przez /(«) rozumieli dowolną funkcję ciągłą, dla «> 0,

11) Udowodnić, że

ff(jL+ JL)i_nx*L ₌ i_na {/(*. + ±\ŚL _(a>0),

J \a x/ x    J \a x/ x

o    o

jeżeli tylko całki są zbieżne.

Wskazówka. Dokonać podstawienia x = ae“ (a = — oo, /? = + oo).

12) Udowodnić, że (dla p>0):

(a) f f(x'+x-’) ln x ~~ = 0,    (b) f f(x’+x~>) ln *    = 0,

O    o

jeżeli tylko całki są zbieżne.

oo 1 oo    co    1

Mamy na przykład w przypadku (a) J = J+J, lecz f = — J, o czym łatwo możemy się przekonać,

0    0    1    1    O

dokonując podstawienia x =*    , itd.

13) Udowodnić wzór

«°    g. .    %    2*1    ®

/ ^f[\^Ax~ J ^dx = ~aJ ^{f(y2) dy {A}'^B>0)’

O    O

przy założeniu, że całka po prawej stronie jest zbieżna.

Za pomocą podstawienia y — Ax—— (a = — oo, 6 = -foo, ot = O, p = + oo) otrzymujemy

/ /&■)*—/ /[(-<*--f) ] (^A+^Jk)‘^lx-

o    o

Tę ostatnią całkę możemy jednak za pomocą podstawienia x = —B/At (a = O, b = +a>, a = — <x>, p «* 0) sprowadzić do

A

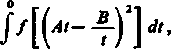
—co