0534

536

XIII. Całki niewłaściwe

to

(4b)    J    — dx = /( + oo)lny.

o

Nawiasem mówiąc, ten przypadek sprowadza się do poprzedniego przez podstawienie

x

1_

t

496. Całki z funkcji wymiernych w granicach nieskończonych. Rozpatrzmy wreszcie jeszcze jedną szczególną postać całki w granicach nieskończonych

+00

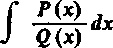
gdzie P(x) i Q(x) są wielomianami. Załóżmy, że wielomian Q(x) nie ma pierwiastków rzeczywistych i że stopień wielomianu P(x) jest co najmniej o dwie jednostki mniejszy niż stopień Q(x). Przy tych założeniach całka istnieje [474, 2)], chodzi tylko o jej obliczenie.

Jeśli x_x = a_x+iPji (Pt. > 0 ^b P_x < 0 i A = 1,2,...) są różnymi pierwiastkami wielomianu Q(x), to ułamek P (x)jQ(x) można w następujący sposób rozłożyć na ułamki proste

(5)

P(x)

Q(x)

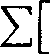
Aą

x-x_3L

+

Aa

(x~x_x)²

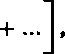
przy czym liczba ułamków w każdym nawiasie jest równa krotności odpowiedniego pier* wiastka (*).

Uogólniając na przypadek funkcji zespolonej zmiennej rzeczywistej elementarne sposoby obliczania całek widzimy od razu, że dla m> 0 jest

+00

/

—00

dx

(x-x_xyⁿ+^l

L

m

1 !+oo

(x-x_x)^m I-® “ ° ’

a więc

+00

I

P(x)

Q(x)

dx

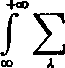
———dx = lim X~x_x *-+oo

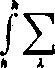
Aa

x-x_x

dx .

(‘) W rozdziale VIII [274] mieliśmy już podobne rozwinięcie, lecz tam staraliśmy się nie brać pod uwagę pierwiastków urojonych iw przypadku takich pierwiastków rozpatrywaliśmy ułamki, których mianownikami były potęgi trójmianu kwadratowego już o współczynnikach rzeczywistych. Tutaj zaś pierwiastki urojone traktujemy na równi z rzeczywistymi.