0558

560

XIII. Całki niewłaściwe

Jeżeli a> 1 i jc<0, to sprawa znacznie się komplikuje. W tym przypadku też możemy otrzymać wzo¹ ry (13)-(16), lecz wszystkie całki musimy rozumieć w sensie wartości głównych. Wyrazy szeregu (16) będą miały w tym przypadku stały znak (przecież ¹<0) i przy szacowaniu reszty natrafimy na duże trudności. Za pomocą dokładnych i głębokich badań udało się Stieltjesowi wykazać, że aby otrzymać najlepsze przybliżenie wartości li (e~^x) należy dla danego ¹<0 wziąć także n — [|x|J. Stopień przybliżenia szacuje się

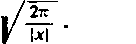
przy tym przez

Możemy otrzymać dla funkcji li (e~^x) rozwinięcie według całkowitych rosnących potęg x, słuszne dla wszystkich wartości x. Napiszemy w tym celu wzór (13) w postaci

li (<?-¹) - j    f e~'~+ jJ(l-e-')-y-.

0    0 10

c lit

Gdy x<0, całka J —jest rozbieżna i trzeba wziąć jej wartość główną. Jest ona równa

i ¹

t    X    _    _

lim ( ( + f) — = lim I ln e+ln    i = In (—x) = ln |.v|.

«-,+o% ¹    •-►+0 L • J

Suma pierwszych dwóch całek nie zależy od x i jest równa stałej C(‘). Pozostaje tylko rozwinąć ostatnią całkę według potęg x, żeby otrzymać szukany wynik

(17)

li(e-) = C+ln Ul—jf— -~

x³ x⁴

31-3    41-4

ni n

Jednak korzystać z tego rozwinięcia dla dużych wartości |x| nie jest wygodnie i szereg rozbieżny (16) ma w tym przypadku nad nim wyraźną przewagę. Stieltjes obliczył, biorąc 23 wyrazy szeregu (16), że

li io¹⁰ = 455055614,586;

natomiast w szeregu (17) trzeba by wziąć ponad 10¹⁰ wyrazów, żeby uzyskać tę samą dokładność!

2° Kosinus i sinus całkowy:

P = cix = - f    Q = six = — j -5iD-Ldt.

X    X

W celu uproszczenia rozważań rozpatrzymy całkę z funkcji zespolonej zmiennej rzeczywistej

P+Qi=- flldt^t f¹1.

•>    t    J    t

X    X

Kolejnym całkowaniem przez części otrzymamy wzór

₀tx    ₀ix    ₀ix    ₀ix    ₀lK

^f+el " TT ⁺ W ⁺2!mr^+,'iPr ⁺'    +'•<->•

gdzie

00

r,(x) = (-iy-‘i" n!- f -~^-dt.

1

Jak zobaczymy później, jest ona rzeczywiście równa stałej Eulera [538, 3)].