241 (23)

—

Rozdział 5.

Układy regulacji impulsowej

Uwaga¹ o sposobie określania równania charakterystycznego dla liniowych układów impulsowych.

Schemat rozpatrywanego układu impulsowego przedstawiono na rys. 5.1.

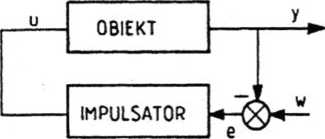
Rys. 5.1. Schemat blokowy układu impulsowego

Zakładamy, iż obiekt może być przedstawiony w ten sposób, że nie występują w nim sprzężenia zwrotne (A (s) = 1, patrz p.2.2). Oznaczmy przez m₃ (z), j — 1,2, ...,fc mianowniki dyskretnych transmitancji poszczególnych k bloków tego schematu. Przyjmujemy, że sygnał wyjściowy impulsatora jest określony następująco:

u(t) = a(t — nTi) e (nT_t) dla nTi < t < (n + 1) Ti

gdzie:

a (ł — nTi) - wektor współczynników wagowych,

T - okres impulsowania.

Oznaczmy przez K (z) dyskretną transmitancję macierzową układu otwartego

Y (z) = K (z) E (z).

Można wykazać, że równanie charakterystyczne badanego układu zamkniętego przyjmuje

postać:

k

det [I + K (z)] mj (z) = 0 j=i

przy warunku det [/ + K (oo)j / 0.

1

Autorem tej uwagi jest M. Latarnik