470 2

470

12. Rozwiązania zadań

§ 4.5

1.    Dla £(/)=$>,/00 wybieramy jako/dowolną funkcję z C^l taką, :te/(*j_=sw_,

i H/IU-1-

Dia L (/) = 3/(0) - 2/( 1) przyjmujemy f(x) = 1 - 2x*.

i

Dla Z. (/) = j e~^xf(x) dx przyjmujemy /(*) = I. o

Dla L(0=/(0)+/'(0) rozważamy ciąg funkcji /,=sin (/nrx),    cos (/nur). Jcfli

n-*oo, to L(f_n)-*cc i ponieważ ||/,||_fl0=l, więc ||Z.|| = oo.

2.    T-

3.    (b) 0.222, 0.25 (wykorzystać własność minimaksu wielomianów Czebyszewal).

4.    8“^l/2—£, (/)=0.0214 (zob. zadanie 1 z § 4.4 i zadanie 5 z § 4.5).

S-lhW-13*); 0.0278.

6.    0.000007 - 0.999479* -0.249870*³ 4 0.057837*³ + 0.010764*⁴

7.    (*-2)/(2x+l).

8.    Z twierdzenia 4.5.1 i wzoru Stirlinga

(*)

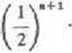
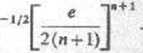
Zastosowanie twierdzenia Bernsteina: Dłuższa oś elipsy ws-pomnianej w twierdzeniu jest równa HR+ljjR). Stąd

(•*)    E_m(f)ś2MR-'(R^z-iy¹'² = 2exp{łR)R~<^m+¹⁾(l+0(R-¹)).

Dla danego w ostatnie wyrażenie jest najmniejsze dla /?=»+!. Stąd

(i+o(«r^ł)).

r-—T

L2(n + l)J

Oszacowania (*) i (**) są dość podobne, a pierwsze z nich jest lepsze (dodatkowy czynnik: e[2K(n + l)]-¹¹²).

Najlepsze zastosowanie twierdzenia Jacksona otrzymuje się dla fc=n. Wtedy

EJU)<e

(* + !)!'

Oszacowanie jest gorsze od poprzednich około n* razy.

Dla n=13:    twierdzenie 4.5.1 =» £₁₃(/)50.4 10^-14,

twierdzenie Bernsteina =»• E_lz{f)<, 1.3-10”¹⁴, twierdzenie Jacksona => £₁₃(/);S 10“ ⁸.

9. Niech będzie L(f)= Y (— l)*a*/(cos [£*/(«+1)]). Jest oczywiste, że »+i    *-o    .

= Z |aj~*+l. Wobec twierdzenia 4.5.2 wystarczy wskazać, że L(/)=0 dla /C*J