504 2

504

12. Rozwiązania zadań.

if abs (R)<e.px then go to out;

T[k, /+!]:« H*. r]+i?/(2tf/+l)-l) end cnd aut:

4.    (a) (1 —A)", (b) 0<A<2.    (c)

5.    h_fnnx = 2ik.

§ 8.3

1. Różniczkowanie daje y ^u (0) = i\ (/= 1,2, ...). Szereg Taylora:

>>(*)=!+x+x² + ...

Szereg ma promień zbieżności 1, nie nadaje się zatem do obliczenia v(1.2). Dokładne rozwiązanie

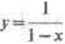
(x<L)

ma asymptotę pionową dla x= I; tłumaczy to, dlaczego szereg nie jest dobry' dla x> I. Dla .*=0 2, korzystając ze składników do x^fi, otrzymujemy y— 1.25000; zauważmy, że

\r_t\ś ^ ^ = 16-10^-6, «_CJ = I6-I0"⁶,    |K|<(l6-t-16)-10"⁶<0.5*I0"⁴.

2. Oto sensowny sposób wykonania obliczeń:

h=0.2 x	y	y	k-hy'
0	i	i	0.2
0.1	u	1.2	0.24
0.1	1.12	1.22	0.244
0.2	1.244	1.444	0.2888
>>(0.2)= l +£(0-24 0.48 + 0.488 + 0.2888) =			1.242800.
A=0.1 0	1	1	0.1

0.05 0.05 0.1	1.05 1.055 l.l 105	l.l 1.105 1.2105	0.11 0.1105 0.12105
0.1	1.110342	1.210342	0.121034
0.15	I.P0859	1.320859	0.132086
0.15	1.176385	1.326385	0.132638
0.2	I.2429SO	1.442980	0.144298
0.2	1.242805

Ekstrapolacja:y(0.2)= 1.242805 l 5-10“⁶/(f6— l) = 1.242805. Dokładna wartość: 2e⁰'²—1.2 - 1.242806± 10^-t’.