62 (186)

192 ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

538. &L i ^l*fr^>192 192

539. a) Wierzchołki: 51, krawędzie: 100. ściany: 51; b) 8.

541. 20.

540. b) 140cm²: c) lA-Jl cni'.

542. Objęłoś: xa ', pole powierzchni: ^/ra*.

543.

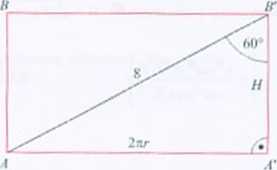
Rozwiązanie. Oznaczenia: II - wysokość walca, r promień podstawy walca. Na rysunku obok pokazano powierzchnię boczną walca po rozwinięciu na płaszczyznę - prostokąt A4 BK. Długość jednego boku lego prostokąta jest równa długości wysokości walca (inaczej: illugoici tworzącej walca), a długość drugiego boku jest równa obwodowi podstawy walca, czyli jest równa 2?tr.

W trójkącie

s/T_2 to _r_ 2&.

sinhO

2®1 8

Ir

f A'

cosóO® = -—, stąd II 4. Obliczamy objętość walca: V = xr~łl = zr--^-4 = —.

" “ ” ' X² *

546. I2V3/r.

544. Pole: Xr² . Objętość: ±xr³tga . 545. a) 2^2: b) 72rr.

547. 5n.

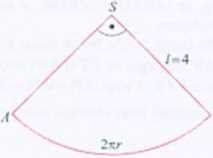
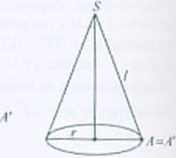
Rozwiązanie. < tznaczenia: / - tworząca stożka, r - promień podstawy stożka. Na rysunku obok pokazano powierzchnię boczną stożka po rozwinięciu na płaszczyznę wycinek AA’S. Długość promienia tego wycinka jest równa długości tworzącej stożka, a długość luku. na którym oparty jest wycinek jest równa obwodowi podstawy stożka, czyli jest równa 2xr.

Ponieważ kąt środkowy wycinka jest kątem prostym, więc długość luku AA’ jest równa ’ i obwodu koła o promieniu 4 (dany wycinek jen „ćwiartką" kola

o promieniu 4). Zatem: 2zrr = -jt2zr 4i. a stąd r = I. Obliczamy pole powierzchni całkowitej P, stożka: P, = n? + .rr/ = .?+ 4,t= 5zr.

548.

<i\r\ t/7^:

I92.T* -jn" “

(przyjęliśmy, ze a jest miarą kąta wyrażoną w rnd łanach i.

549. 2yfir.

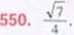
Rozwiązanie. (tznaczenia: r - promień stożka. I - tworząca stożka, h - wysokość stożka. R promień walca. // - wysokość (tworząca) walca. Wiemy, ze 0/ = //. 0 ±xr²h ■ x R^: H. © jnl = IrMH. Z O i 0 mamy: xrH = 2xRH. stąd r = 2R. Podstawiając do 0 otrzymujemy

^xAR~h--xR~H, stąd Ii = Ąh. Ponieważ /' = r~ + /i’. więc r' =l~ - Ir = II ~ -(—//)" = — //“, siad ,₌2^L//_

•’ 4 4 16 4

551. 30°.

Rozwiązanie. Oznaczenia: r-promień stożka. /- tworząca stożka, h - wysokość stożka, a- kąt między tworzącą, a wysokością stożka. Przekrój osiowy .stożka to trójkąt równoramienny o podstawie Ir i wysokości h. Pole przekroju osiowego stożka jest więc równe rh. Wiemy, zc rhx4i x r~ +/tri, stąd * lifi = r + l. j = sinrr natomiast j = coso. stąd re/sina, h - lensa. Pb podstawieniu do * i po podzieleniu

obu stron przez. I dostajemy równanie trygonometryczne Jicosa = sin« + I. Przekształcamy: V3 cosa-.sina = I. —-cosec --sint* = —,

sin60° co* a -co*60® kina = ~, sin(60° -a i = (ze wzoru na sinus różnicy). Ponieważ O jest kątem ostrym, więc z ostatniej równości wynika, że 60" - cr^ 30". czyli (t - 30 ‘.