8097134324

50

Marek Beska, Całka Stochastyczna, wykład 4

gdzie

<HX) =

X + V(X) 2

*{X) =

V(X) - X 2

Z (4.1) procesy 4>(X) i il’{X) są rosnące. Zatem X £ V. Załóżmy teraz, że X £ V, to X = Ai — A2 dla Ai £ V⁺, i = 1,2. Oba procesy A\ i A2 są procesami rosnącymi, mają skończone wahanie, więc X ma skończone wahanie. Ponadto Xo = 0 i X jest adaptowany jako różnica dwóch procesów adaptowanych.

□

Niech A £ V⁺ i niech X będzie takim procesem, że dla oj £ fi trajektorie t    u)

są borelowskie. Dla ui £ f2 odwzorowanie [0, (] 3 s 4 ^4s(^w) określa dodatnią skończona miarę na [0, £]. Możemy rozważyć całkę

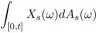
jeśli dla w trajektoria X^(uj) jest całkowalna względem A(.)(o;). Taka całka jest faktycznie całką Lebesgue’a-Stieltjesa

f X_s(u})dA_a(u) = f X_s(co)dA_s(io). J[0,t]    J o

Możemy również określić dla A £ V jeśli

/ X,{u)dA_s(u)

Ąo,t]

( |X_s|d(P(yl)_s) < +00.

J[o,t]

Wtedy

f X_sdA_s := f X_sd<f>{A)_s - f X_sdip(A)_s J[o,t)    J[o,t]    J[o,t]

Lemat 4.5 Niech A £ V i niech X będzie dowolnym procesem dla którego trajektorie X(.)(w), u £ fi są całkowalne (skończenie) na przedziale [0, t] dla t > 0 względem A_s(u) to całka Lebesgue’a-Stieltjesa (proces)

Y_t(u)= [ X_s(oj)dA_s{u) Jo

jest cad i ma skończone wahanie.

Dowód. Własność cad procesu Y wynika z własności cad procesu A oraz z własności całki Lebesgue’a-Stieltjesa. Oznaczmy

X⁺ = XV0, X~ = (-X)V0, wtedy X = X⁺ - X~.