8097134325

Marek Beska, Całka Stochastyczna, wykład 4

51

oraz

U_t =    [ X+d<j)(A)a + f X~dip(A)_s

'o    Jo

rt    rt

W_t= X+dip(A)_s + / X~d<f>(A).

są procesami rosnącymi i skończonymi na przedziale [0, t] dla t > 0. Zatem mają skończone wahanie, a stąd proces Y = U — W ma także skończone wahanie.

□

Zauważmy, że proces Y otrzymaliśmy biorąc całkę Lebesgue’a-Stieltjesa dla każdej trajektorii oddzielnie i dlatego nie ma powodów aby Y był adaptowany, opcjonalny czy prognozowalny. Żeby otrzymać powyższe własności musimy założyć coś więcej.

Lemat 4.6 Zachodzą następujące fakty:

1. Niech A e V. Jeśli X jest opcjonalny i całka Lebesgue’a-Stieltjesa

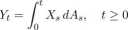
istnieje (i jest skończona), to Y jest opcjonalny.

2. Niech A G V. Jeśli X i A są prognozowalne i całka Lebesgue’a-Stieltjesa

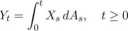
istnieje (i jest skończona), to Y jest prognozowalny.

Dowód. Przystąpmy do dowodu 1. Zauważmy najpierw, że A e V jest opcjonalny oraz V(A) jest też opcjonalny (bo V(A) jest cadlag i adaptowany), a więc 4>(A) i if(A) są też opcjonalne. Stąd jeśli zastąpimy A przez <t>(A) i ip(A) to wystarczy wykazać nasz lemat dla elementów z V⁺. W dowodzie zastosujemy twierdzenie o klasach monotonicznych. Niech

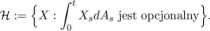
Zauważmy, że U spełnia założenia twierdzenia o klasach monotonicznych, bo

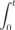
Yt — lcŁ4_s — At — Aq- — At — opcjonalny =*> 1 e H

i H jest zamknięta na monotoniczne granice. Jako klasę multiplikatywną wystarczy przyjąć zbiór indykatorów przedziałów stachastycznych [[5, oo[[, gdzie S jest czasem zatrzymania.