262080025

Wykłady z Ekonometrii Opracował: dr Adam Kucharski

Jeżeli spojrzeć na to szerzej, nie powinniśmy sprawiać wrażenia zaskoczonych. Zjawiska ekonomiczne podlegają w niektórych okresach (takich jak wojny czy gwałtowne recesje lub boom gospodarczy) raptownym wahaniom. Przyjmują wtedy wartości skrajnie odbiegające od okresów, które w tej sytuacji można nazwać „normalnymi” lub typowymi. Wyróżnimy 3 grupy takich nietypowych zachowań:

1.    obserwacje nietypowe występujące w pojedynczych, nieregularnych okresach;

2.    obserwacje nietypowe trwające przez kilka okresów z rzędu;

3.    obserwacje nietypowe regularnie się powtarzające.

Zazwyczaj nie jesteśmy w stanie zrezygnować z danych dotyczących nietypowych okresów. Ewentualne skrócenie próby ma daleko idące konsekwencje podczas estymacji. Z drugiej strony brak kroków zaradczych oznacza modele o słabych własnościach statystycznych i merytorycznych. Jako wyjście proponuje się stosowanie zmiennych zero-jedynkowych. Zmienną taką definiuje się następująco:

{0, dla obserwacji typowych;

(18)

1, dla obserwacji nietypowych.

Zmienne zero-jedynkowe tworzone są więc sztucznie, zgodnie z naszymi potrzebami⁷. Wprowadza się je następnie do równania i szacuje parametry w tradycyjny sposób. W zależności od użycia mogą one wywoływać zmianę któregoś z pozostałych parametrów w wybranych okresach. Równanie (19) prezentuje korektę wyrazu wolnego:

Yi = «o + o/*₀Ui + a.iXi + £i    (19)

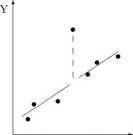
Rysunek 7: Zmienna zero-jedynkowa dla wyrazu wolnego Niekiedy należy zmienić współczynnik kierunkowy równania:

Yi = a₀ + (c*i + (ĄUi)Xi +    (20)

Sytuację z równania (20) ilustruje rysunek 8.

Możliwe jest również połączenie rozwiązań zaproponowanych w (19) oraz (20) dla jednego modelu.

'Należy jednak zachowywać umiar przy wprowadzaniu zmiennych zero-jedynkowych. Ich użycie musi być odpowiednio umotywowane.

12 z 26