262080041

Wykłady z Ekonometrii Opracował: dr Adam Kucharski

1.    Jeżeli |t_a<| > tkryt wówczas (przy przyjętym z góry poziomie istotności) odrzucamy Hq na korzyść H\. Zmienna objaśniająca w istotny sposób wpływa na zmienną objaśnianą.

2.    Jeżeli |t_Qj| < tkryt wówczas (przy przyjętym z góry poziomie istotności) nie mamy podstaw do odrzucenia hipotezy zerowej, a więc uznajemy dany parametr za nieistotny statystycznie.

Konsekwencje braku istotności są bardzo poważne. Oznaczają bowiem, że umieszczona w równaniu zmienna objaśniająca znalazła się tam niepotrzebnie. W takiej sytuacji należy ją usunąć i dokonać reestymacji równania.

3.3 Autokorelacja składnika losowego

Z autokorelacją mamy do czynienia, kiedy składniki losowe dotyczące różnych obserwacji są ze sobą skorelowane. Z taką sytuacją spotykamy się najczęściej w przypadku szeregów czasowych. Przyczyny występowania autokorelacji są różne:

1.    natura procesów gospodarczych np serie klęsk trwające przez wiele okresów;

2.    wpływ zdarzeń najbliższej przeszłości na podejmowane decyzje;

3.    niepoprawna postać funkcyjna modelu np nie uwzględnienie cyklu gospodarczego;

4.    wadliwa struktura dynamiczna modelu: brak opóźnionych zmiennych w charakterze zmiennych objaśniających;

5.    pominięcie ważnej zmiennej objaśniającej.

Najpoważniejszą konsekwencją występowania autokorelacji jest obciążenie estymatora wariancji składnika losowego. Kierunek obciążenia bywa różny. Dla autokorelacji dodatniej wariancja ta jest niedoszacowana co prowadzi do pozornie większej dokładności ocen parametrów. W konsekwencji otrzymujemy zawyżone statystyki t-Studenta.

Najczęściej zakłada się występowanie schematu autoregresyjnego pierwszego rzędu (tzw schemat AR(1)), w którym występuje powiązanie między składnikami losowymi z sąsiednich okresów:

(13)

e_t = pe_t-1 + r)t

gdzie:

p - współczynnik autokorelacji;

Vt ~ N{0, a_v)

Szczególną własnością zjawisk ekonomicznych jest to, że pozostają one ze sobą zawsze w jakimś związku. Z tego powodu autokorelacja, choć niepożądana, jest właściwie nie do uniknięcia. Nasze działania zmierzają więc po pierwsze do określenia siły autokorelacji, a następnie do podjęcia decyzji odnośnie przeciwdziałania jej skutkom.

Najprościej byłoby policzyć współczynnik autokorelacji, lecz należy pamiętać, iż nie znamy wprost składnika losowego. Z tego powodu po raz kolejny wykorzystamy jego przybliżenie czyli reszty z modelu. Niestety oznacza to, że możemy poznać jedynie estymator wartości p. Istnieje kilka sposobów na obliczenie p:

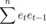
t=2

Pi =

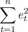
(14)

9 z 26