138

274 XIII. Badanie przebiegu zmienności funkcji
274 XIII. Badanie przebiegu zmienności funkcji
Punk.
Zadanie 13.6. Zbadać przebieg zmienności funkcji y=ell(l~*2>-Rozwiązanie. Funkcja jest określona dla 1 — x2^Q, tzn. dla x¥^-\ i 1. W tach nieokreśloności znajdujemy granice funkcji (patrz zad. 5.13):
lim /(jc) = 0, lim/(*)=+oo, lim /(*)= +oo , lim f(x) = Q.
x—-1 — O x—-1+0 *-1-0 *-1+0
Widzimy, że proste x=-l i x=l są asymptotami pionowymi krzywej. Następnie obliczamy granice funkcji dla x-+-oo i dla jr-+ + co:
lim /(*)= lim f(x) = 1.
X~* “00 X— + 00
Widzimy, że prosta p=l jest dwustronną asymptotą poziomą krzywej.
Obliczmy pierwszą pochodną
1/11 -**)
, 2x
y =-5“i e
(I — x2)~
Pochodna równa się zeru, gdy jr = 0; wtedy /(0) = e. Pochodna jest ujemna, gdy jc<0, a dodatnia, gdy jc>0.
Obliczamy granice pochodnej, gdy *-+-1-0, x-»- 1 + 0, x--l - O i x->l+0. Mamy
,= -2 lim
1
lim f'(x)= lim 2x lim - , ,
*--i-o *--i-o *-»-i —o(l — x ) *— -1 -o (1 — x )
,i/(i-*2»
Aby obliczyć ostatnią granicę, dokonujemy podstawienia 1/(1 -x2)= -u; zauważmy, że gdy x —► — 1 — O, to -u-* — oo, a więc u-» + oo. Mamy więc
lim f\x)=-2 lim -*-,el/n xlj=-21im--
*—i-o *-,-,_0(1-jc2)2 „-+«, e“
u2
Ale w myśl wyników otrzymanych w zadaniu 12.7 mamy lim —=0 więc
u-* + CO £
lim /(jc) = 0.
*--i-o
Aby obliczyć lim f(x), dokonujemy podstawienia 1/(1— x2) = u i otrzymujemy
*--1 + ó
lim f(x)——2 lim u2e“=— co.
jc-* — 1+0 u -* + co
Podobnie postępując otrzymujemy
lim /'(+)=+ oo, lim f’(x) = 0. *-i-o *-i+o
Obliczamy drugą pochodną
y
» 2(3
(l-x2)4
uga pochodna jest równa zeru, gdy 3x*- 4x2— 1 =0. Podstawiając x2 = t(t> 0) otrzy-" >mv równanie kwadratowe 3r2-4/-1 =0, które ma jeden pierwiastek dodatni t=
iiiUP J /--—
^(L + yJl)- A więc miejscami zerowymi drugiej pochodnej są xt = -vi(2 + N/7) i *2 =
^'*(2 + 7+
funkcja ma przerwy ciągłości w punktach x= — 1 i jc = 1, przy czym przy x dążącym j0 każdej z tych wartości jedna gałąź krzywej jest styczna do osi Ox, a druga asympto
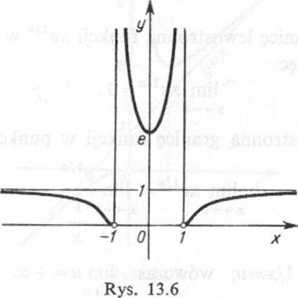
tycznie zbliża się do prostej x= — 1 lub x=\. Funkcja jest symetryczna względem osi Oy i osiąga minimum w punkcie x = 0. Krzywa ma dwa punkty przegięcia.
Układamy tabelkę przebiegu zmienności danej funkcji:
|
X |
— co |
... |
X\ |
-i |
... |
0 |
i |
... |
Xl |
... |
+ 00 | ||||
|
y" |
0 |
- |
0 |
+ |
0 |
— CO |
_L |
+ |
+ |
— oo |
0 |
+ |
0 |
- |
0 |
|
y |
0 |
- |
- |
- |
0 |
— 00 |
- |
0 |
+ |
+ co |
0 |
+ |
+ |
+ |
0 |
|
y |
i |
\ |
/(* i) |
0 |
+ 00 |
\ |
e |
y |
+ CO |
0 |
/ |
/(**) |
y |
1 | |
Wykres funkcji podaje rysunek 13.6.
Zadanie 13.7. Zbadać przebieg zmienności funkcji y=xel/x. Rozwiązanie. Funkcja jest określona dla *#0.
Obliczmy pochodną
P
y'=e1,x+xe'/x ( —V) = e1,x—— eł/x = -—-\ X J X X
°chodna jest równa zeru w punkcie x = \; wtedy /(l)=e. Obliczamy drugą pochodną
e
l/x
y" = el,x
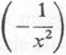
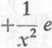
l/x
1
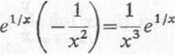
Wyszukiwarka
Podobne podstrony:
136 2 270 XIII. Badanie przebiegu zmienności funkcji Układamy tabelkę przebiegu zmienności danej
142 2 282 XIII. Badanie przebiegu zmienności funkcji X1 13.28. y = exl~1 . 13.29. y = e~x2 • 13.3
8 Badanie przebiegu zmienności wybranych funkcjiZestaw 8. Badanie przebiegu zmienności wybranych
Badanie przebiegu zmienności funkcjiDEFINICJE, TWIERDZENIA Zanim zaczniemy badać przebieg zmienności
035 4 Badanie przebiegu zmienności funkcji Twierdzenie: Asymptota ukośna Prosta y = ca + b je
Badanie przebiegu zmienności funkcji czyli lim f(x) = -oo Brak asymptot poziomych. Asymptota pionowa
Badanie przebiegu zmienności funkcji6-7. Monotoniczność i ekstrema funkcji 2xi - 2 sgn f (x) = sgn--
039 2 Badanie przebiegu zmienności funkcji 3. Parzystość i nieparzystość
043 5 Badanie przebiegu zmienności funkcji 2. Punkty wspólne z osiami OX, OY. oś OX Badanie przebieg
Badanie przebiegu zmienności funkcji x e (-co; -1) =>/(.x) 71 je(-];0) =>/(*) x e (0; 1)
045 2 Badanie przebiegu zmienności funkcji Asymptota ukośna f(x) ~X^ "ł" 2 A 2 y
094 2 186 X. Badanie przebiegu zmienności funkcji 10.3. Funkcja /(x) =
095 2 188 X. Badanie przebiegu zmienności funkcji § 10.4. WYPUKŁOŚĆ 1 WKLĘSŁOŚĆ FUNKCJI Niech będą d
096 2 190 X. Badanie przebiegu zmienności funkcji Krzywa jest wszędzie wypukła (bo _y">0) i
097 2 192 X. Badanie przebiegu zmienności funkcji Wykreślamy krzywą y = x3 + 3x2 —9x — 2 (rys. 10.8,
098 2 194 X. Badanie przebiegu zmienności funkcji Zadanie 10.11. Zbadać przebieg zmienności funkcji
099 2 196 X. Badanie przebiegu zmienności funkcji asymptotą pionową krzywej y=f(x); natomiast gdy *-
Pochodna funkcji. Badanie przebiegu zmienności funkcji. Całka nieoznaczona, całkowanie przez części
więcej podobnych podstron