142 2

282 XIII. Badanie przebiegu zmienności funkcji

X¹

13.28. y = e^xl~^1 .	13.29. y = e~^x2 •
13.30. y = e-^xl + 8x~'* ■	13.31. y = xe~^ixl.
13.32. y = x^2e^Ux .	13.33. y = xV^4*.
13.34. y=(a+^J e^x,a.	13.35. y=sje^x2~ 1 .
13.36. y = e^tsx.	13.37. y=e^aTCttx .
13.38. y = e^arcsinJx .	13.39. _>/ = arctg(Inx)

OBLICZANIE PRZYBLIŻONYCH WARTOŚCI PIERWIASTKÓW RÓWNAŃ I UKŁADÓW RÓWNAŃ

§ 14.1. METODA CIĘCIW

Dane jest równanie /(x) = 0. Niech f(x) będzie funkcją ciągłą, która w końcach przedziału a^x^b przybiera wartości różniące się znakiem, np./(a)<0, f(b)>0 (rys. 14.1). Oznaczmy końce łuku krzywej w tym przedziale przez A i B.

Robimy jednocześnie następujące założenia:

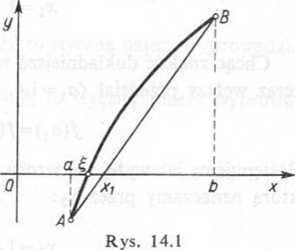
1.    Niech pierwsza pochodna w przedziale a<x<b zachowuje stały znak; wówczas f(x) jest ściśle monotoniczna i przecina oś Ox dokładnie jeden raz. .

2.    Niech druga pochodna będzie w tym przedziale różna od zera; wówczas linia y=f(x) nie ma punktów przegięcia w tym przedziale.

Można udowodnić metodami algebry, że każdy przypadek da się sprowadzić do takiego, w którym te założenia są spełnione.

Metoda poszukiwania pierwiastka równania zwana metodą cięciw (lub metodą podziału 1'oporcjonalnego albo reguła falsi) polega na tym, że za przybliżoną wartość pierwiastka zawartego w tym przedziale przyjmujemy odciętą punktu przecięcia cięciwy AB z osią Ox

(a

Uwaga. W przypadku gdy stosowana jest metoda cięciw, można by drugie założenie

'^a Podaną dalej metodę kombinowaną.

Równanie cięciwy AB, jako prostej przechodzącej przez punkt A(a,f(a)) i B(b,f(b)),

nawet pierwsze) usunąć, zachowujemy je jednak dla ułatwienia, a także ze względu

tot

,,, m-m, ,

>’-/0)= —r-(x-a).

b-a

Xi = a-f(a)

Mawiając y-0 otrzymujemy odciętą x_L punktu przecięcia cięciwy AB z osią Ox: '^•l.l)    .. . b-a

m-m

I ^Jist ta

⁰ Przybliżona wartość pierwiastka równania.