Matematyka 2 75

374 V. Elementy rachunku pruwilopodobieństM o

P( U < 1.33) = d>( 1,33) = 0.90K2 * 0.91. wartość tą odczytujemy z tablicy la, znajdującej się na końcu książki.

b) szukaną liczbą jest kwantyl: u = u_0ił5 = l,645, (por. rys 6.7), odczytujemy go z tablicy Ib.    ■

TWIERDZENIE 6.1. Jeżeli ZL X ma rozkład normalny N(p,cr), to ZL U postaci

^dcf X—u

(6.11)    U =

a

ma standaryzowany rozkład normalny N(0; 1)

Dowód. Należy sprawdzić, że GP tp ZL U jest postaci (6.7). Niech F i f oznaczają dystiybuantą i GP ZL X o rozkładzie N(p.o). Wyrazimy najpierw dystrybuantę ZL U za pomocą dystrybuanty F ZL X:

4>(u)= P(U<u)= P(^—^-<u)= P(X<p+cru) = F(p+(ju).

(T

Różniczkując teraz dystrybuantę cl) względem zmiennej u, otrzymamy GP cp ZL U:

ę> (u) = cl)' (u) = [ F (p + <ju ) ]' = F ’ (p + ou) • er = o f (p + au) =

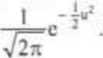
I Iłit-nił-ur

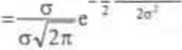
n

Przekształcenie (6.11) dokonane na ZL X nazywa się. jak wiemy, standaryzowaniem ZL X Ostatnie twierdzenie umożliwia więc, drogą standaryzacji ZL X o rozkładzie N(p,a), wyznaczanie różnych pr-stw dotyczących ZL X za pomocą dystrybuanty <b ZL U o rozkładzie N(0.1). Nu przykład:

(6.12)    P(a<X<b) = cb(-^)-d>(^±!);

ci    o

w szczególności dla a = -x, b=+oc mamy

(6.13)    P(X<b)=<P(-^i!'), PCX>a) = 1-dH²—^iŁ)-

o    a

Równość (6.12) otrzymujemy w rezultacie następującego ciągu równości:

P(a<X<b)=P(—<^lH.<^i)= o cj a

=P, iizit < u < hzŁ)₌_ <1>Ą

o    a    er    er

PRZYKŁAD 6.2. ZL X ma rozkład N(5,2). Wyznaczy-my: a) P(X<5), b)P(4<X<5), c) P(|X|<4), d) P(|X-4|>2).

c) P(3X-X²>0),

a)    Krzywa gęstości ZL X jesi symetryczna wzglądem prostej s = 5. zatem, bez korzystania z tablic, mamy: P(X<5) = 0,5

b)    Kolejno na mocy (6.12) i (6.9) otrzymujemy:

P(4 < X < 5) = 0(    - <D(^) = 0(0) - 0>( -0.5) =

= 0.5-[l-(I><0.5)]=0.5-1+0.6915=0.1915*0.19;

c)    P(JXJ<4) = P(-4< X <4)i

= <tH-0,5)-<J>(-4.5) = I -<l>(0,5)-0 = 1-0,6915 = 0.3085*0,31;

d)    P(|X-4i>2) = I — P(1X—4|<2) = I — P(—2<X—4<2) =

= l-P(2<X<6)=l-(O(03)-a»(-l,5)l=l-[a>(0,5)-l+cl)(1.5)]«= =2-0(O.5)-d>(l,5)=2-O,6915-0,9332=0,3755*0,38; c) P(3X-X^:>0) = P(0<X<3) = <D(-l)-<t>(-2,5) =

= l-O(l)-1 +0(2.5) = 0,9938-0.8413=OJ 525* 0.15;

0 P(|-<l) = P(X<0albo X>5) = P(X<0)+P(X>5) =

= O(-2.5)+0.5 = l-O(2,5) +0.5= 1,5-0.9938 = 0.5062 *0,51.

ZADANIA DO ROZWIĄZANIA

1 U/asadnic prawdziwość wzorów (6.2) na wartość oczekiwaną i wariancją ZL o rozkładzie prustokątnym. Wyznaczyć dystrybuantą F tej ZL.

2. Autobusy z przystanku miejskiej linii odjeżdżają co 8 minut Chwila przyjścia pasażera na przystanek może być traktowana jako wartość ZL. Sensownie jest założyć, że ta 7.L ma rozkład prostokątny. Przy tym założeniu obliczyć pr-stwo. że pasażer bądzie czekał na autobus co najwyżej 3 minuty.

0 dla t<0

3. ZL T o GP postaci f(t) =

1 .^5 ^ _{^ ^ jest dobrym modelem

dla czasu bezawaryjnej pracy pewnego urządzenia. Obliczyć: