SWScan00079

Konthaksy tsrmwowe 1 OPCJE

Tabela 5.J Obliczanie omh li wadia obligacji
Cm	Płatność	Wartość bieżąca	Waga	Czas X Waga
0.5	5	4.709	0,050	0.025
t.O	5	4.435	0.047	0.047
1.3	5	4.176	0,044	0.066
2.0	5	3.933	0.042	0,084
2.5	5	3,704	0,039	0,098
3.0	105	73.256	0,778	2.334
Karem	130	94,213	1.000	2.654

Przykład

Rozważmy trzyletnią, dziesięcioprocentową obligację kuponową o wartości no-tmoalnci 100 dolarów. Przyjmijmy. że stopa zwrotu z tej oWięacil przy kapitalizacji ciągłej wynusl 12 ptucciil noczu.it:, a więc y- Oj 2. Dochody kuponowe w wysokości 5 dolarów wypłacone są en szieść miesięcy "tobola 5.5 przedstawia ohl-.czenia niezbędne du określenia czasu trwania. Wartość hieżąca ptarności, gdzie jako >tupa dyskontowa przyjęta z usiała stupa zwrotu z obligacji, przedstawiona jert w kolumnie trzeciej. Przykładowo: wnrtnść bieżąca pierwszej płatności wy:ioai 4.709 ( ~ S.- *^iłaj). Pu zsumowaniu wszystkich wartości w tej kn-lunude otrzymujemy cenę obligacji tówuą 94.213 dolana. Wag: ubliczone zostały poprzez. podzielenie poszczególnych wartości z kolumny trzeciej przez cenę obligacji - 94,213. Suma wartości z kolumny piątej daje czas trwania równy 2,654 lat. Z zalcżnoicl (5.9):

AB = -94,213 x 2,654Ay

czyli

Aił = —25Q04Ay

JclU Ay -■►0,001, to y wzrośnie do 0,121. * z powyższej zależności wynika, żc oczekujemy Ail rOwmgu 0.25 Innymi słowy, spodziewamy się. że cena obligacji spadnie du poziomu 93.963 (- 94,213- 0.25). W cele sprawdzenia po-wyższych rozważań czytelnik może obliczyć cenę obligacji dla stopy zwrotu równej 12.1 procent.

Czas trwania portfela obligacji można zdefiniować jako średnią ważoną czasów trwania poszczególnych obligacji składowych portfela, gdzie wagi są p<t)|Kiiv'jnnalne do ceny obligacji. Zależność (5.9) można żalem stosować zarówno do pojedynczych obligacji, jak i do całego portfela, pod warunkiem jednak, że slupy zwrotu wszystkich obligacji wchodzących w skład porrfcla zmieniają się w tnła sam sposób.

Dotychczasowa analiza opierała się oa /ułożeniu, że y podlega kapitalizacji ciągłej. Jeśli y jest kapitalizowane rocznic, to zależność (5.9) można zapisać jaku:

BDby

Procentowe kontrakty fulures

145

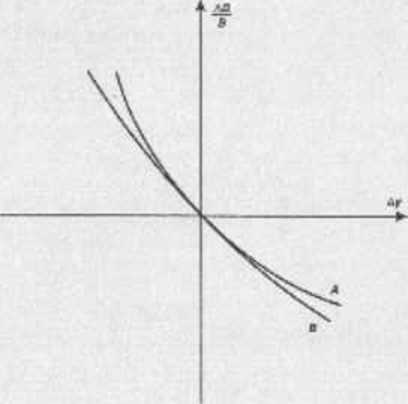
DLaęrasn 5JS Portfele obligacji o rrtł.ncj wypakknicl.

Uogólniając, jeśli y podlega kapitalizacji m razy w noku, ic>:

PI

gdzie wyrażenie:

D

l + Z

>n

bywa określane jako zmodyfikowany etos trwoniła {mndijlcd dumfioń).

Harmonizacja czasu trwania i wypukłość

Portfel papienW wiinościowych o stałym dochodzie może być określony zn pomocą swojego czasu trwania. Instytucje nmuisuwe ęzęsUi próbują /niwnui czas trwania swoich aktywów z czasem trwania swoich zobowiązań (zobowiązania można traktować jako krótką pozycję w obbgacinch). Procedura tu, znana pod nnzwą harmonizacji cyuu (rwania {durauoii matekbtft) luh immunizocłi portfela (portfulia immunization). opiera się na założeniu, że krzywa dochodowości przesuwa się zawsze równolegle Jeśli czasy trwania aktywów 1 /ubu wiązań «ą /.liarmonizowime, to niewielka równoległa zmiana stóp procentowych powinna mleć niewielki wpływ na w;irii»ć całego portfela. /. zależności (5.9) wynika, że zysk z aktywów powinien być zrównoważony pracz stratę na zobowiązaniach i odwrotnie.